
【题目】已知:如图所示,点E在直线DF上,点B在直线AC上,∠A=50°,∠AGB=∠EHF,∠C=∠D,求∠F的度数.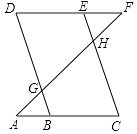
 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() 的图像交于(1,3),B(3,n)两点.
的图像交于(1,3),B(3,n)两点. 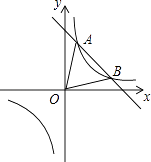
(1)求一次函数和反比例函数的解析式;
(2)连接AO,BO,求△ABO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 四个角相等的菱形是正方形 B. 对角线垂直的四边形是菱形
C. 有两边相等的平行四边形是菱形 D. 两条对角线相等的四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义了一种新运算T,规定T(x,y)= ![]() (其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)= ![]() ,已知T(1,﹣1)=﹣2,T(4,2)=1.
,已知T(1,﹣1)=﹣2,T(4,2)=1.
(1)求a,b的值;
(2)若关于m的不等式组 ![]() 恰好有3个整数解,求p的取值范围.
恰好有3个整数解,求p的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线 ![]() 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且
与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 ![]() ,则k的值是( )
,则k的值是( )
A.4
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A2处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015,到BC的距离记为h2015.若h1=1,则h2015的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个等边三角形木框,甲虫P在边框AC上爬行(A,C端点除外),设甲虫P到另外两边的距离之和为d,等边三角形ABC的高为h,则d与h的大小关系是( ) 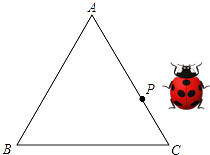
A.d>h
B.d<h
C.d=h
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com