
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
【答案】
(1)解:设去年A型车每辆售价x元,则今年售价每辆为(x﹣200)元,由题意,得
![]() =
= ![]() ,
,
解得:x=2000.
经检验,x=2000是原方程的根.
答:去年A型车每辆售价为2000元
(2)解:设今年新进A型车a辆,则B型车(60﹣a)辆,获利y元,由题意,得
y=(1800﹣1500)a+(2400﹣1800)(60﹣a),
y=﹣300a+36000.
∵B型车的进货数量不超过A型车数量的两倍,
∴60﹣a≤2a,
∴a≥20.
∵y=﹣300a+36000.
∴k=﹣300<0,
∴y随a的增大而减小.
∴a=20时,y最大=30000元.
∴B型车的数量为:60﹣20=40辆.
∴当新进A型车20辆,B型车40辆时,这批车获利最大
【解析】(1)设去年A型车每辆售价x元,则今年售价每辆为(x﹣200)元,由卖出的数量相同建立方程求出其解即可;(2)设今年新进A型车a辆,则B型车(60﹣a)辆,获利y元,由条件表示出y与a之间的关系式,由a的取值范围就可以求出y的最大值.


科目:初中数学 来源: 题型:
【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
租金(单位:元/台时) | 挖掘土石方量(单位:m3/台时) | |
甲型挖掘机 | 100 | 60 |
乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车队要把4000吨货物运到雅安地震灾区(方案定后,每天的运量不变)。
(1)从运输开始,每天运输的货物吨数n(单位:吨)与运输时间t(单位:天)之间有怎样的函数关系式?
(2)因地震,到灾区的道路受阻,实际每天比原计划少运20%,则推迟1天完成任务,求原计划完成任务的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形![]() 的边长为2,
的边长为2,![]() =60°,对角线
=60°,对角线![]() ,
,![]() 相交于点O.以点O为坐标原点,分别以
相交于点O.以点O为坐标原点,分别以![]() ,
,![]() 所在直线为x轴、y轴,建立如图所示的直角坐标系.以
所在直线为x轴、y轴,建立如图所示的直角坐标系.以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,,按此规律继续作下去,在x轴的正半轴上得到点
,,按此规律继续作下去,在x轴的正半轴上得到点![]() ,
,![]() ,
,![]() ,......,
,......,![]() ,则点
,则点![]() 的坐标为________.
的坐标为________.
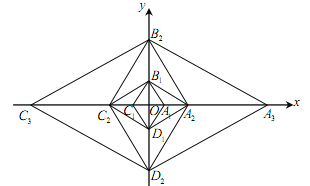
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,0),B(3,0),C(0,2),CD∥x轴,CD=AB.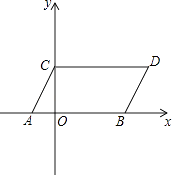
(1)求点D的坐标:
(2)四边形OCDB的面积S四边形OCDB;
(3)在 y轴上是否存在点P,使S△PAB=S四边形OCDB?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若方程ax2+bx+c=0(a≠0)中,a,b,c满足a+b+c=0和a﹣b+c=0,则方程的根是( )
A. 1,0 B. ﹣1,0 C. 1,﹣1 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,BO平分∠ABC,CO平分∠ACB,MN过点O,交AB于M,交AC于N,且MN∥BC,若AB=12cm,AC=18cm,则△AMN周长为 . 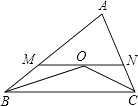
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com