
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E、F为圆心,大于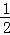 EF的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠ACD=120°,则∠MAB的度数为 .
EF的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠ACD=120°,则∠MAB的度数为 .
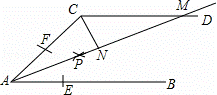
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.
(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;
(2)当点C在直线BE上时,连接FC,直接写出∠FCD的度数;
(3)如图3,如果α=45°,AB=2,AE=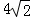 ,求点G到BE的距离.
,求点G到BE的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于 CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )
CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )

A. SAS B.ASA C.AAS D. SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中,∠C=90°,∠A=30°.
(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.

查看答案和解析>>
科目:初中数学 来源: 题型:
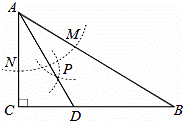
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于 点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线
②∠ADC=60°
③点D在AB的垂直平分线上
④AB=2AC.
A. 1 B.2 C.3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
(如图,在△ABC中,BC=AC,且CD∥ AB,设△ABC的外心为O.
AB,设△ABC的外心为O.
(1)用尺规作出△ABC的外接圆O.(不写作法,保留痕迹)
(2)在(1)中,连接OC,并证明OC是AB的中垂线;
(3)直线CD与⊙O有何位置关系,试证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com