练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一次函数y＝﹣2x+6的图象与x轴的交点坐标是_____．

    【答案】（3，0）

    【解析】

    y＝0，即可求出x的值，即可求解.

    解：当y＝0时，有﹣2x+6＝0，

    解得：x＝3，

    ∴一次函数y＝﹣2x+6的图象与x轴的交点坐标是（3，0）．

    故答案为：（3，0）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

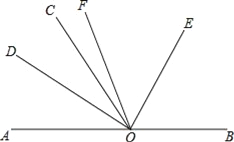
    【题目】如图，点O为直线AB上一点，过点O作直线OC，已知∠AOC≠90°，射线OD平分∠AOC，射线OE平分∠BOC，射线OF平分∠DOE．求：

    （1）当0°＜∠AOC＜90°时，求∠FOB+∠DOC的度数；

    （2）若∠DOC=3∠COF，求∠AOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

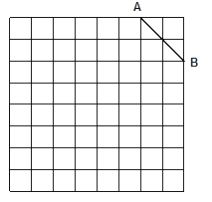
    【题目】如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作：

    ⑴ 请在网格中建立平面直角坐标系, 使A点坐标为(2，4)，B点坐标为(4，2)；

    ⑵ 请在（1）中建立的平面直角坐标系的第一象限内的格点上确定点C, 使点C与线段AB组成一个以AB为底的等腰三角形, 且腰长是无理数, 则C点坐标是 ， △ABC的周长是 (结果保留根号)；

    ⑶ 以（2）中△ABC的点C为旋转中心、旋转180°后的△A′B′C, 连结AB′和A′B, 试说出四边形ABA′B′是何特殊四边形, 并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数据4402万用科学记数法表示正确的是( )

    A. 4.402×107 B. 44.02×108 C. 44.02×107 D. 4.402×108

    查看答案和解析>>

    科目：初中数学 来源： 题型：

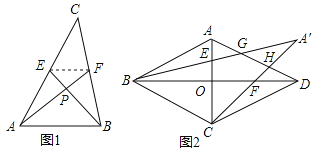
    【题目】尤秀同学遇到了这样一个问题：如图1所示，已知AF，BE是△ABC的中线，且AF⊥BE，垂足为P，设BC=a，AC=b，AB=c．

    求证：．

    该同学仔细分析后，得到如下解题思路：

    先连接EF，利用EF为△ABC的中位线得到△EPF∽△BPA，故，设PF=m，PE=n，用m，n把PA，PB分别表示出来，再在Rt△APE，Rt△BPF中利用勾股定理计算，消去m，n即可得证．

    （1）请你根据以上解题思路帮尤秀同学写出证明过程．

    （2）利用题中的结论，解答下列问题：

    在边长为3的菱形ABCD中，O为对角线AC，BD的交点，E，F分别为线段AO，DO的中点，连接BE，CF并延长交于点M，BM，CM分别交AD于点G，H，如图2所示，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】x＝1是方程2x＋a＝－2的解，则a的值是（ ）

    A. －4 B. －3 C. 0 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系上有点A（1，0），点A第一次跳动至点A1（﹣1，1），第二次向右跳动3个单位至点A2（2，1），第三次跳动至点A3（﹣2，2），第四次向右跳动5个单位至点A4（3，2），……，依此规律跳动下去，点A第2018次跳动至点A2018的坐标是______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列多项 式相乘的结果是a2-a-6的是（　　）
    A.（a-2）（a+3）
    B.（a+2） （a-3）
    C.（a-6）（a+1）
    D.（a+6）（a-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在“爱我永州”中学生演讲比赛中，五位评委分别给甲、乙两位选手的评分如下：

    甲：8、7、9、8、8

    乙：7、9、6、9、9

    则下列说法中错误的是（ ）

    A．甲、乙得分的平均数都是8

    B．甲得分的众数是8，乙得分的众数是9

    C．甲得分的中位数是9，乙得分的中位数是6

    D．甲得分的方差比乙得分的方差小

    查看答案和解析>>

    同步练习册答案