
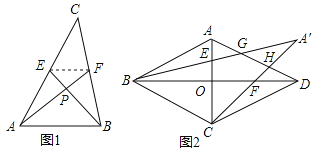
【题目】尤秀同学遇到了这样一个问题:如图1所示,已知AF,BE是△ABC的中线,且AF⊥BE,垂足为P,设BC=a,AC=b,AB=c.
求证:![]() .
.
该同学仔细分析后,得到如下解题思路:
先连接EF,利用EF为△ABC的中位线得到△EPF∽△BPA,故![]() ,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证.
,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证.
(1)请你根据以上解题思路帮尤秀同学写出证明过程.
(2)利用题中的结论,解答下列问题:
在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图2所示,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)5.
【解析】
试题分析:(1)设PF=m,PE=n,连结EF,如图1,根据三角形中位线性质得EF∥AB,EF=![]() c,则可判断△EFP∽△BPA,利用相似比得到PB=2n,PA=2m,接着根据勾股定理得到
c,则可判断△EFP∽△BPA,利用相似比得到PB=2n,PA=2m,接着根据勾股定理得到![]() ,
,![]() ,则
,则![]() ,而
,而![]() ,所以
,所以![]() ;
;
(2)利用(1)的结论得![]() =
=![]() =45,再利用△AEG∽△CEB可计算出AG=1,同理可得DH=1,则GH=1,然后利用GH∥BC,根据平行线分线段长比例定理得到MB=3GM,MC=3MH,然后等量代换后可得
=45,再利用△AEG∽△CEB可计算出AG=1,同理可得DH=1,则GH=1,然后利用GH∥BC,根据平行线分线段长比例定理得到MB=3GM,MC=3MH,然后等量代换后可得![]() =5.
=5.
试题解析:(1)设PF=m,PE=n,连结EF,如图1,∵AF,BE是△ABC的中线,∴EF为△ABC的中位线,AE=![]() b,BF=
b,BF=![]() a,∴EF∥AB,EF=
a,∴EF∥AB,EF=![]() c,∴△EFP∽△BPA,∴
c,∴△EFP∽△BPA,∴![]() ,即
,即![]() =
=![]() ,∴PB=2n,PA=2m,在Rt△AEP中,∵
,∴PB=2n,PA=2m,在Rt△AEP中,∵![]() ,∴
,∴![]() ①,在Rt△AEP中,∵
①,在Rt△AEP中,∵![]() ,∴
,∴![]() ②,①+②得
②,①+②得![]() ,在Rt△EFP中,∵
,在Rt△EFP中,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
(2)∵四边形ABCD为菱形,∴BD⊥AC,∵E,F分别为线段AO,DO的中点,由(1)的结论得![]() =
=![]() =45,∵AG∥BC,∴△AEG∽△CEB,∴
=45,∵AG∥BC,∴△AEG∽△CEB,∴![]() ,∴AG=1,同理可得DH=1,∴GH=1,∴GH∥BC,∴
,∴AG=1,同理可得DH=1,∴GH=1,∴GH∥BC,∴![]() ,∴MB=3GM,MC=3MH,∴
,∴MB=3GM,MC=3MH,∴![]() ,∴
,∴![]() =5.
=5.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】为了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体统计如下:
阅读时间(小时) | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时的众数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点A(2,5),B(﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是___________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把方程3x(x+1)=2(x–2)+8化为一般形式______,二次项系数______,一次项系数__________,常数项______。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”。
(1)请问一元二次方程x2-3x+2=0是倍根方程吗?如果是,请说明理由。
(2)若一元二次方程ax2+bx-6=0是倍根方程,且方程有一个根为2,求a、b的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
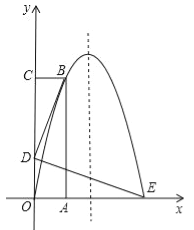
【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;
(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com