练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】为了解学生暑期在家的阅读情况，随机调查了20名学生某一天的阅读小时数，具体统计如下：

    阅读时间（小时）

    2

    2.5

    3

    3.5

    4

    学生人数（名）

    1

    2

    8

    6

    3

    则关于这20名学生阅读小时的众数是_____．

    【答案】3．

    【解析】

    众数是一组数据中出现次数最多的数据，根据众数的定义就可以求出．

    在这一组数据中3出现了8次，出现次数最多，因此这组数据的众数为3．

    故答案为：3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】计算m2+2m2的结果是（ ）

    A. 2m4 B. 3m2 C. 3m4 D. 2m2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以下说法正确的是（ ）

    A. 一次摸奖活动的中奖率是1%，那么摸100次奖必然会中一次奖；

    B. 一副扑克牌中，随意抽取一张是红桃K，这是必然事件；

    C. 一个不透明的袋中装有3个红球，5个白球，任意摸出一个球是红球的概率是．

    D. 必然事件的概率为1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

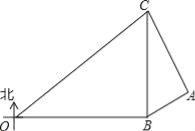
    【题目】在某次海上军事学习期间，我军为确保△OBC海域内的安全，特派遣三艘军舰分别在O、B、C处监控△OBC海域，在雷达显示图上，军舰B在军舰O的正东方向80海里处，军舰C在军舰B的正北方向60海里处，三艘军舰上装载有相同的探测雷达，雷达的有效探测范围是半径为r的圆形区域．（只考虑在海平面上的探测）

    （1）若三艘军舰要对△OBC海域进行无盲点监控，则雷达的有效探测半径r至少为多少海里？

    （2）现有一艘敌舰A从东部接近△OBC海域，在某一时刻军舰B测得A位于北偏东60°方向上，同时军舰C测得A位于南偏东30°方向上，求此时敌舰A离△OBC海域的最短距离为多少海里？

    （3）若敌舰A沿最短距离的路线以20海里/小时的速度靠近△OBC海域，我军军舰B沿北偏东15°的方向行进拦截，问B军舰速度至少为多少才能在此方向上拦截到敌舰A？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个圆内接正六边形的一边所对的圆周角为( )

    A. 60° B. 120° C. 60°或 120° D. 30°或150°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

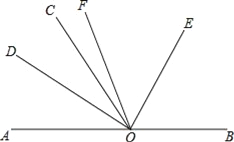
    【题目】如图，点O为直线AB上一点，过点O作直线OC，已知∠AOC≠90°，射线OD平分∠AOC，射线OE平分∠BOC，射线OF平分∠DOE．求：

    （1）当0°＜∠AOC＜90°时，求∠FOB+∠DOC的度数；

    （2）若∠DOC=3∠COF，求∠AOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

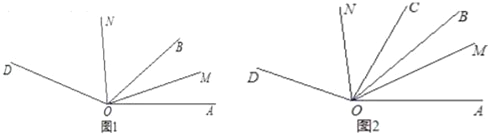
    【题目】已知：∠AOD=160°，OB、OC、OM、ON是∠AOD内的射线，

    （1）如图1，若OM平分∠AOB，ON平分∠DOB，当OB绕点O在∠AOD内旋转时，求∠MON的大小．

    （2）如图2．若∠BOC=20°，OM平分∠AOC，ON平分∠DOB，当∠COB绕点O在∠AOD内旋转时，求∠MON的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图， 中，∠=90°，是斜边上的中线，分别过点作∥， ∥，两线交于点.

    （1）求证：四边形是菱形；

    （2）若， ，求四边形的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

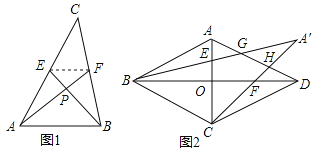
    【题目】尤秀同学遇到了这样一个问题：如图1所示，已知AF，BE是△ABC的中线，且AF⊥BE，垂足为P，设BC=a，AC=b，AB=c．

    求证：．

    该同学仔细分析后，得到如下解题思路：

    先连接EF，利用EF为△ABC的中位线得到△EPF∽△BPA，故，设PF=m，PE=n，用m，n把PA，PB分别表示出来，再在Rt△APE，Rt△BPF中利用勾股定理计算，消去m，n即可得证．

    （1）请你根据以上解题思路帮尤秀同学写出证明过程．

    （2）利用题中的结论，解答下列问题：

    在边长为3的菱形ABCD中，O为对角线AC，BD的交点，E，F分别为线段AO，DO的中点，连接BE，CF并延长交于点M，BM，CM分别交AD于点G，H，如图2所示，求的值．

    查看答案和解析>>

    同步练习册答案