
【题目】已知:∠AOD=160°,OB、OC、OM、ON是∠AOD内的射线,
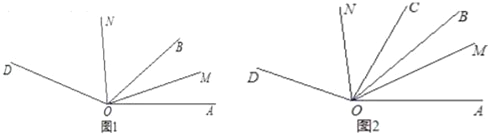
(1)如图1,若OM平分∠AOB,ON平分∠DOB,当OB绕点O在∠AOD内旋转时,求∠MON的大小.
(2)如图2.若∠BOC=20°,OM平分∠AOC,ON平分∠DOB,当∠COB绕点O在∠AOD内旋转时,求∠MON的大小.
【答案】(1)80°;(2)70°
【解析】(1)根据角平分线的定义求出∠BOM和∠BON,然后根据∠MON=∠BOM+∠BON代入数据进行计算即可得解;
(2)设∠AOB=x,表示出∠BOD=α-x,根据角平分线的定义表示出∠COM和∠BON,然后根据∠MON=∠COM+∠BON-∠BOC列式计算即可得解.
(1)∵∠AOD=160°,OM平分∠AOB,ON平分∠BOD
∴∠MOB=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD
∠BOD
即∠MON=∠MOB+∠BON=![]() ∠AOB+
∠AOB+![]() ∠BOD=
∠BOD=![]() (∠AOB+∠BOD)
(∠AOB+∠BOD)
=![]() ∠AOD=80°;
∠AOD=80°;
(2)∵OM平分∠AOC,ON平分∠BOD
∴∠MOC=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD
∠BOD
即∠MON=∠MOC+∠BON﹣∠BOC=![]() ∠AOC+
∠AOC+![]() ∠BOD﹣∠BOC
∠BOD﹣∠BOC
=![]() (∠AOC+∠BOD)﹣∠BOC=
(∠AOC+∠BOD)﹣∠BOC=![]() ×180°﹣20°
×180°﹣20°
=70°
“点睛”本题考查了角的计算,角平分线的定义,准确识图是解题的关键,难点在于要注意整体思想的利用.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
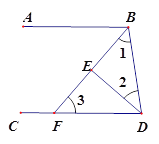
【题目】如图,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F,∠1+∠2=90°.试问直线AB,CD在位置上有什么关系?∠2与∠3在数量上有什么关系?并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校测量了全校800名男生的身高,并进行了分组,已知身高在1.70~1.75(单位:m)这一组的频率为0.25,则该组共有男生( )
A. 100名B. 200名C. 250名D. 400名
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体统计如下:
阅读时间(小时) | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时的众数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年1—5月份,深圳市累计完成地方一般预算收入216.58亿元,数据216.58亿精确到( )
A. 百亿位 B. 亿位 C. 百万位 D. 百分位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把方程3x(x+1)=2(x–2)+8化为一般形式______,二次项系数______,一次项系数__________,常数项______。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com