
【题目】某校课外小组为了解同学们对学校“阳光跑操”活动的喜欢程度,抽取部分学生进行调查.被调查的每个学生按A(非常喜欢)、B(比较喜欢)、C(一般)、D(不喜欢)四个等级对活动评价.图(1)和图(2)是该小组采集数据后绘制的两幅统计图.经确认扇形统计图是正确的,而条形统计图尚有一处错误且并不完整.请你根据统计图提供的信息,解答下列问题:

(1)此次调查的学生人数为 ;
(2)条形统计图中存在错误的是 (填A、B、C中的一个),并在图中加以改正;
(3)在图(2)中补画条形统计图中不完整的部分;
(4)如果该校有600名学生,那么对此活动“非常喜欢”和“比较喜欢”的学生共有多少人?
【答案】(1)200;(2)C;改正图形略;(3)补全图形略;(4)360人.
【解析】试题分析:(1)根据A、B的人数和所占的百分比求出抽取的学生人数,并判断出条形统计图A、B长方形是正确的;
(2)根据(1)的计算判断出C的条形高度错误,用调查的学生人数乘以C所占的百分比计算即可得解;
(3)求出D的人数,然后补全统计图即可;
(4)用总人数乘以A、B所占的百分比计算即可得解.
试题解析:解:(1)∵40÷20%=200,
80÷40%=200,
∴此次调查的学生人数为200;
(2)由(1)可知C条形高度错误,
应为:200×(1﹣20%﹣40%﹣15%)=200×25%=50,
即C的条形高度改为50;
故答案为:200;C;
(3)D的人数为:200×15%=30;
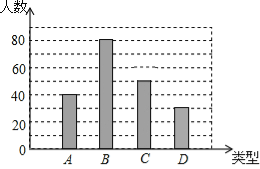
(4)600×60%=360(人).
答:该校对此活动“非常喜欢”和“比较喜欢”的学生有360人.


科目:初中数学 来源: 题型:
【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.

证明:
∵AB∥CD,(已知)
∴∠_____=∠_____.( )
∵ ,(已知)
∴∠EBC=![]() ∠ABC.(角的平分线定义)
∠ABC.(角的平分线定义)
同理,∠FCB= .
∴∠EBC=∠FCB.(等式性质)
∴BE∥CF.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教研机构为了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查.依据相关数据绘制成以下不完整的统计图表,请根据图表中的信息解答下列问题:

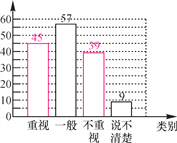
(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2 300名,请估计该校“不重视阅读数学教科书”的初中生人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y1=﹣x+b过点A,且与直线y2=x+3相交于点B(m,2),直线y2=x+3与x轴相交于点C. 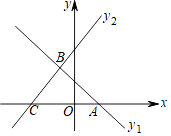
(1)求m的值.
(2)求△ABC的面积.
(3)根据图象,直接写出关于x的不等式﹣x+b>x+3的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
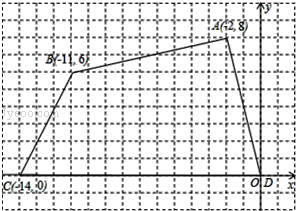
【题目】如图,有一块不规则的四边形图形ABCD,各个顶点的坐标分别为A(﹣2,8),B(﹣11,6),C(﹣14,0),D(0,0),
(1)确定这个四边形的面积
(2)如果把原来四边形ABCD的各个顶点的纵坐标保持不变,横坐标加1,画出平移后的图形。
(3)求出平移后四边形面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的方格纸中,三角形ABC的顶点都在方格纸格点上.将三角形ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的三角形A′B′C′;
(2)再在图中画出三角形ABC的高CD;
(3)在图中能使S三角形PBC=S三角形ABC的格点P有 个(点P异于A).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,辽宁都市频道为此进行过专访报道.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A 非常赞同;B 赞同但要有时间限制;C 无所谓;D 不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.

请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com