
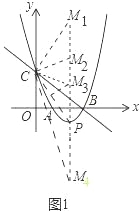
����Ŀ����ͼ�����κ���y=x2+bx+c��ͼ��x����A��B���㣬��y���ڵ�C������Ϊ��P������B��C�����ֱ��Ϊy=��x+3��
��1����ö��κ����Ĺ�ϵʽ��
��2���ڸ������ߵĶԳ������Ƿ���ڵ�M��ʹ�Ե�C��P��MΪ������������ǵ��������Σ������ڣ���ֱ��д�����з��������ĵ�M�����ꣻ�������ڣ���˵�����ɣ�
��3������AC����x�����Ƿ���ڵ�Q��ʹ�Ե�P��B��QΪ��������������ABC���ƣ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1�����κ�������ʽΪy=x2-4x+3����2��M1��2��7����M2��2��2![]() -1����M3��2��
-1����M3��2�� ![]() ����M4��2��-2
����M4��2��-2![]() -1������3�����ڵ�Qʹ���Ե�P��B��QΪ���������������ABC���ƣ���Q���꣨0��0����
-1������3�����ڵ�Qʹ���Ե�P��B��QΪ���������������ABC���ƣ���Q���꣨0��0����![]() ��0����
��0����
�������������������1�������B��C���꣬���������߽���ʽ�ⷽ���鼴�ɽ�����⣮
��2���������������ۼ�����CM=CP����PM=PC����MP=MC������ͼ�μ��ɽ�����⣮
��3���������������ۼ�����![]() ʱ����ABC�ס�PBQ1���г����̼��ɽ��������
ʱ����ABC�ס�PBQ1���г����̼��ɽ��������![]() ʱ����ABC�ס�Q2BP���г����̼��ɽ����
ʱ����ABC�ס�Q2BP���г����̼��ɽ����
�����������1����ֱ��y=-x+3����B��C���㣬
��B��3��0����C��0��3����
�����κ���y=x2+bx+cͼ��x����A��B���㣬��y���ڵ�C��
��![]() ���
���![]() ��
��
�����κ�������ʽΪy=x2-4x+3��
��2����y=x2-4x+3=��x-2��2-1��
���������ߵĶԳ���Ϊֱ��x=2����������ΪP��2��-1����
����ͼ1��ʾ�����������ĵ�M�ֱ�Ϊ
M1��2��7����M2��2��2![]() -1����M3��2��
-1����M3��2�� ![]() ����M4��2��-2
����M4��2��-2![]() -1����
-1����
��3���ɣ�1����2����A��1��0����BP=![]() ��BC=3
��BC=3![]() ��AB=2��
��AB=2��
��ͼ2��ʾ������BP����CBA=��ABP=45����
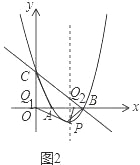
��![]() ʱ����ABC�ס�PBQ1��
ʱ����ABC�ס�PBQ1��
��ʱ�� ![]()
��BQ1=3��
��Q1��0��0����
����![]() ʱ����ABC�ס�Q2BP��
ʱ����ABC�ס�Q2BP��
��ʱ�� ![]() ��
��
��BQ2=![]() ��
��
��Q2��![]() ��0����
��0����
�������������ڵ�Qʹ���Ե�P��B��QΪ���������������ABC���ƣ���Q���꣨0��0����![]() ��0����
��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2020����Űȫ����¹ڲ����Ĵ�СΪ0.000000125�ף��ÿ�ѧ��������ʾΪ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��̣��ף�������˾������12�������ɣ����踶ʩ����102000Ԫ������ף�������˾������ɴ���̣��ҹ�˾����ʱ���Ǽ�˾��1.5�����ҹ�˾ÿ���ʩ���ѱȼ�˾ÿ���ʩ������1500Ԫ��
��1���ף�������˾������ɴ���̣���������죿
��2������һ����˾�����������̣��ĸ���˾��ʩ���ѽ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪�ڡ�ABC��,AB=AC,������������,����ʹBD=CE����( )
A.BD��CE�ֱ�ΪAC��AB���ϵ�����
B.BD��CE�ֱ�Ϊ��ABC�͡�ACB��ƽ����
C.BD��CE�ֱ�ΪAC��AB���ϵĸ�
D.��ABD=��BCE
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ı���ABCD��������,��PAD�ǵȱ�������,���BPC����( )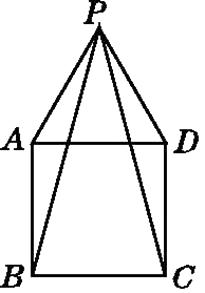
A.20��
B.30��
C.35��
D.40��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ABC�ǵȱ�������,D�DZ�BC��(��B,C��)������һ��,��ADE=60��,��DE����ACF��ƽ����CE�ڵ�E.��֤: 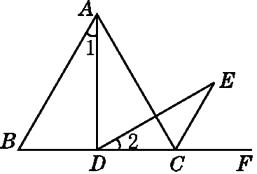
��1����1=��2;
��2��AD=DE.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˱�ս2016����Լ���˻ᣬ�й���������ڻ���ѵ�����ס��������˶�Ա����ͬ�������£������10�Σ��������㣬�ס������˳ɼ���ƽ��������9.5�����ijɼ�������0.125���ҵijɼ��ķ�����0.85����ô��10������У��ס��ҳɼ����ȶ�����ǣ� ��
A.��Ϊ�ȶ�
B.�ҽ�Ϊ�ȶ�
C.�����˳ɼ�һ���ȶ�
D.����ȷ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com