
【题目】如图,△ABC是等边三角形,D是边BC上(除B,C外)的任意一点,∠ADE=60°,且DE交∠ACF的平分线CE于点E.求证: 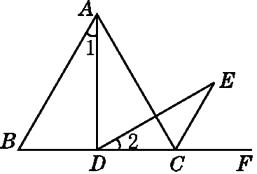
(1)∠1=∠2;
(2)AD=DE.
【答案】
(1)证明:∵△ABC是等边三角形,∠ADE=60°,
∴∠ADE=∠B=60°.
又∵∠ADC=∠2+∠ADE=∠1+∠B,∴∠1=∠2
(2)证明:如图,在AB上取一点M,使BM=BD,连接MD.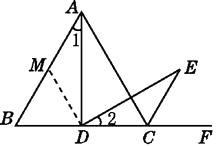
∵△ABC是等边三角形,
∴∠B=60°.
∴△BMD是等边三角形,
∴∠BMD=60°,
∴∠AMD=120°.
∵CE是∠ACF的平分线,
∴∠ECA=60°,
∴∠DCE=120°.
∴∠AMD=∠DCE=120°,
∵ AB=BC ,BM=BD,
∵BA-BM=BC-BD,
∴MA=CD.
在△AMD和△DCE中, 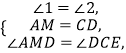
∴△AMD≌△DCE(ASA).
∴AD=DE 。
【解析】 (1)根据等边三角形的性质及已知得出∠ADE=∠B=60°,根据三角形的外角定理及角的和差得出∠ADC=∠2+∠ADE=∠1+∠B,从而得出∠1=∠2 ;
(2)根据等边三角形的性质得出∠B=60°,根据有一个角为60°的等腰三角形是等边三角形得出△BMD是等边三角形 ,等边三角形三个内角都是60°及邻补角的定义得出∠AMD=120°,根据角平分线的定义及角的和差得出∠DCE=120°,从而得出∠AMD=∠DCE=120°,根据等式的性质得出MA=CD,从而利用ASA判断出△AMD≌△DCE,利用全等三角形对应边相等得出AD=DE。


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=x2+bx+c的图象交x轴于A、B两点,交y轴于点C,顶点为点P,经过B、C两点的直线为y=﹣x+3.
(1)求该二次函数的关系式;
(2)在该抛物线的对称轴上是否存在点M,使以点C、P、M为顶点的三角形是等腰三角形?若存在,请直接写出所有符合条件的点M的坐标;若不存在,请说明理由;
(3)连接AC,在x轴上是否存在点Q,使以点P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是随机事件的是( )
A.购买一张福利彩票,中特等奖
B.在一个标准大气压下,加热水到100℃,沸腾
C.任意三角形的内角和为180°
D.在一个仅装着白球和黑球的袋中摸出红球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B的坐标为( )
A.(﹣1,0)
B.(﹣1,﹣1)
C.(﹣2,0)
D.(﹣2,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.函数y=-x+2中y随x的增大而增大
B.直线y=2x-4与x轴的交点坐标是(0,-4)
C.图象经过(2,3)的正比例函数的表达式为y=6x
D.直线y=- ![]() x+1不过第三象限.
x+1不过第三象限.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=6cm,BC=10cm,点D在线段AC上,且CD=2cm,动点P从BA的延长线上距A点10cm的E点出发,以每秒2cm的速度沿射线EA的方向运动了 ![]() 秒。
秒。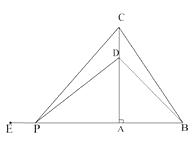
(1)求AD的长;
(2)直接写出用含有 ![]() 的代数式表示PE=;
的代数式表示PE=;
(3)在运动过程中,是否存在某个时刻,使△ABC与△ADP全等?若存在,请求出 ![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com