
【题目】计算下列各式:
(1)1﹣ ![]()
(2)(1﹣ ![]() )(1﹣
)(1﹣ ![]() )
)
(3)(1﹣ ![]() )(1﹣
)(1﹣ ![]() )(1﹣
)(1﹣ ![]() )
)
(4)请你根据上面算式所得的简便方法计算下式:
(1﹣ ![]() )(1﹣
)(1﹣ ![]() )(1﹣
)(1﹣ ![]() )…(1﹣
)…(1﹣ ![]() )(1﹣
)(1﹣ ![]() )…(1﹣
)…(1﹣ ![]() )
)
科目:初中数学 来源: 题型:
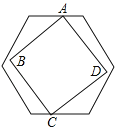
【题目】如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年下半年开始,不同品牌的共享单车出现在城市的大街小巷.现已知A品牌共享单车计费方式为:初始骑行单价为1元/半小时,不足半小时按半小时计算.内设邀请机制,每邀请一位好友注册认证并充值押金成功,双方骑行单价均降价0.1元/半小时,骑行单价最低可降至0.1元/半小时(比如,某用户邀请了3位好友,则骑行单价为0.7元/半小时).B品牌共享单车计费方式为:0.5元/半小时,不足半小时按半小时计算.
(1)某用户准备选择A品牌共享单车使用,设该用户邀请好友x名(x为整数,x≥0),该用户的骑行单价为y元/半小时.请写出y关于x的函数解析式.
(2)若有A,B两种品牌的共享单车各一辆供某用户一人选择使用,请你根据该用户已邀请好友的人数,给出经济实惠的选择建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D
(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,边长为4,点G在边BC上运动,DE⊥AG于E,BF∥DE交AG于点F,在运动过程中存在BF+EF的最小值,则这个最小值是 . 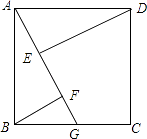
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
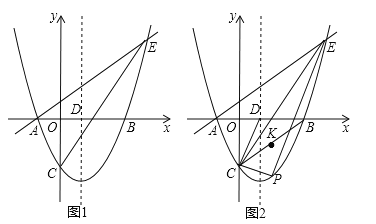
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com