
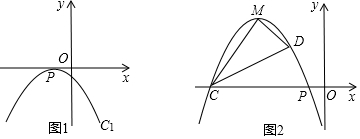
分析 (1)①令x=-1时,可消去解析式中的m,可求得y值为0,可知其过定点,求得P点坐标;②可求得抛物线的顶点坐标,则可用m分别表示出x、y,消去m可求得y与x的函数关系式;
(2)由条件可先求得P点坐标,再结合(1)中所求C2的解析式,可画出图形,由条件可知x轴垂直平分AB,可得到A、B坐标所满足的方程,可求得直线l的方程;
(3)作△PCD和△MCD的两条高线DH和MN,根据条件求点C、P、M、D的坐标,由若S△PCD=S△MCD,列等式可以求出m的值,并根据“抛物线C1的顶点M在第二象限,交x轴于另一点C,抛物线上点M与点P之间一点D”进行取舍,代入解析式中即可.
解答 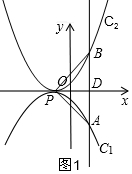 解:(1)①当x=-1时,y=-$\frac{1}{2}$-m+m+$\frac{1}{2}$=0,
解:(1)①当x=-1时,y=-$\frac{1}{2}$-m+m+$\frac{1}{2}$=0,
∴无论m取何值,抛物线经过定点P(-1,0);
y=-$\frac{1}{2}$x2+mx+m+$\frac{1}{2}$=-$\frac{1}{2}$(x-m)2+$\frac{1}{2}$m2+m+$\frac{1}{2}$,
顶点坐标为(m,$\frac{1}{2}$m2+m+$\frac{1}{2}$),
∵顶点M(x,y),y是x的函数,
则其函数C2关系式为:y=$\frac{1}{2}{x}^{2}+x+\frac{1}{2}$=$\frac{1}{2}$(x+1)2;
故答案为:①(-1,0);②y=$\frac{1}{2}{x}^{2}+x+\frac{1}{2}$;
(2)∵该抛物线C1与x轴仅有一个公共点,
∴△=${m}^{2}-4×(-\frac{1}{2})(m+\frac{1}{2})$=0,
m2+2m+1=0,
m1=m2=-1,
∴抛物线C1关系式为:y=-$\frac{1}{2}{x}^{2}$-x-$\frac{1}{2}$=-$\frac{1}{2}$(x+1)2,
如图1,抛物线C1、C2关于x轴对称,
∵△PAB是等腰直角三角形,
∴PA=PB,PA⊥PB,
∵x轴⊥AB,
∴x轴是AB的垂直平分线,
∴BD=PD,
当直线l在顶点P的右侧时,$\frac{1}{2}(x+1)^{2}$=x+1,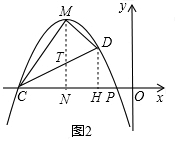
解得x=1,x=-1(不能构成三角形,舍去),
当直线l在顶点P的左侧时,有$\frac{1}{2}(x+1)^{2}$=-x-1,
解得x=-3、x=-1(不能构成三角形,舍去),
则直线l为:x=1或x=-3;
(3)如图2,
当x=-2时,y=-$\frac{1}{2}$×4-2m+m+$\frac{1}{2}$=-m-$\frac{3}{2}$,
∴D(-2,-m-$\frac{3}{2}$),
当y=0时,-$\frac{1}{2}$x2+mx+m+$\frac{1}{2}$=0,
x2-2mx-2m-1=0,
解得:x1=1,x2=2m+1,
∴P(-1,0),C(2m+1,0),
由(1)得:顶点M[m,$\frac{1}{2}$(m+1)2],
过D作DH⊥PC于H,过M作MN⊥PC于N,交CD于T,
则直线CD的解析式为:y=$\frac{1}{2}$x-m-$\frac{1}{2}$,
∴T(m,-$\frac{1}{2}m$-$\frac{1}{2}$),
∵S△PCD=S△MCD,
则$\frac{1}{2}$PC•DH=$\frac{1}{2}$MT•CH,
$\frac{1}{2}$(-1-2m-1)(-m-$\frac{3}{2}$)=$\frac{1}{2}$[$\frac{1}{2}(m+1)^{2}$-$(-\frac{1}{2}m-\frac{1}{2})$](-2-2m-1),
(m+1)(2m+3)=-$\frac{1}{2}$(m+1)(m+2)(2m+3),
(m+1)(2m+3)(m+4)=0,
m1=-1,m2=-$\frac{3}{2}$,m3=-4,
∵抛物线C1的顶点M在第二象限,点D又在点M与点P之间,
∴m1=-1,m2=-$\frac{3}{2}$,不符合题意,舍去,
∴m=-4,
∴y=-$\frac{1}{2}$x2-4x-4+$\frac{1}{2}$=-$\frac{1}{2}$x2-4x-$\frac{7}{2}$,
则二次函数的解析式为:y=-$\frac{1}{2}$x2-4x-$\frac{7}{2}$.
点评 本题是二次函数的综合题,比较复杂,考查了二次函数利用待定系数法求一次函数的解析式、等腰直角三角形的性质,利用配方法求顶点坐标;同时多次运用函数的解析式表示点的坐标,利用方程思想和分类讨论的思想解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
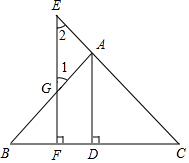 根据下列证明过程填空:
根据下列证明过程填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 木工师傅用刨子可将木板刨平,如图,经过刨平的木板上的两个点,就能弹出一条笔直的墨线,而且只能弹出一条墨线,用数学知识解释其依据为:两点确定一条直线.
木工师傅用刨子可将木板刨平,如图,经过刨平的木板上的两个点,就能弹出一条笔直的墨线,而且只能弹出一条墨线,用数学知识解释其依据为:两点确定一条直线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=x2-3x+$\frac{5}{4}$与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
如图,抛物线y=x2-3x+$\frac{5}{4}$与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com