练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
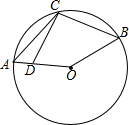
    10．如图，点C在$\widehat{AB}$上，点D在半径OA上，则下列结论正确的是（　　）
    A．∠DCB+$\frac{1}{2}$∠O=180°B．∠ACB+$\frac{1}{2}$∠O=180°C．∠ACB+∠O=180°D．∠CAO+∠CBO=180°

    分析 首先在优弧AB上取点E，连接AE，BE，利用圆周角定理与圆的内接四边形的性质，即可求得答案．

    解答 解：在优弧AB上取点E，连接AE，BE，
    ∵∠E=$\frac{1}{2}$∠O=90°，∠ACB+∠E=180°，
    ∴∠ACB+$\frac{1}{2}$∠O=180°．
    故B正确，A，C，D错误．
    故选B．

    点评 此题考查了圆周角定理以及圆的内接四边形的性质．注意准确作出辅助线是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    20．-6的相反数是6，-$\frac{1}{2}$的倒数是-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图，P为平行四边形ABCD边AD上一点，E，F分别为PB，PC的中点，若S△PEF=2，则S?ABCD=16．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．计算
    （1）（$\sqrt{6}-2\sqrt{15}$）×$\sqrt{3}-6\sqrt{\frac{1}{2}}$
    （2）（3$\sqrt{2}-1$）2-$\root{3}{8}$（4-$\sqrt{72}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．关于x的一元二次方程ax2+bx+c=0（a≠0，b2-4ac＞0）的根是（　　）
    A．$\frac{b±\sqrt{b^2-4ac}}{2a}$B．$\frac{-b+\sqrt{b^2-4ac}}{2a}$C．$\frac{-b±\sqrt{b^2-4ac}}{2}$D．$\frac{-b±\sqrt{b^2-4ac}}{2a}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算：$\sqrt{9}-\root{3}{-8}+4\sqrt{\frac{1}{4}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．数轴上与原点距离为5的点表示的是（　　）
    A．5B．-5C．±5D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

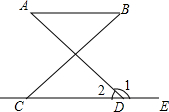    19．在下列推理过程中的括号里填上推理的依据．
    已知：如图，CDE是直线，∠1=105°，∠A=75°．
    求证：AB∥CD．
    证明：∵CDE为一条直线（已知）
    ∴∠1+∠2=180°
    ∵∠1=105°（已知）
    ∴∠2=75°
    又∵∠A=75°（已知）
    ∴∠2=∠A（等量代换）
    ∴AB∥CD（内错角相等两直线平行）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

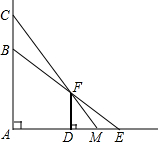    20．如图，一只猫头鹰蹲在树AC上的B处，通过墙顶F发现一只老鼠在E处，刚想起飞捕捉时，老鼠突然跑到矮墙DF的阴影下，猫头鹰立即从B处向上飞至树上C处时，恰巧可以通过墙顶F看到老鼠躲在M处（A、D、M、E四点在同一条直线上）．
    已知，猫头鹰从B点观测E点的俯角为37°，从C点观察M点的俯角为53°，且DF=3米，AB=6米．求猫头鹰从B处飞高了多少米时，又发现了这只老鼠？（结果精确到0.01米）（参考数据：sin37°=cos53°=0.602，cos37°=sin53°=0.799，tan37°=cot53°=0.754，cot37°=tan53°=1.327）．

    查看答案和解析>>

    同步练习册答案