
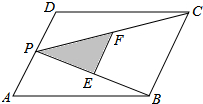
 如图,P为平行四边形ABCD边AD上一点,E,F分别为PB,PC的中点,若S△PEF=2,则S?ABCD=16.
如图,P为平行四边形ABCD边AD上一点,E,F分别为PB,PC的中点,若S△PEF=2,则S?ABCD=16. 分析 利用三角形中位线定理得出EF∥BC,EF=$\frac{1}{2}$BC,再利用相似三角形的判定与性质得出$\frac{{S}_{△PEF}}{{S}_{△PBC}}$=$\frac{1}{4}$,进而利用平行四边形的面积求法得出答案.
解答 解:∵E,F分别为PB,PC的中点,
∴EF∥BC,EF=$\frac{1}{2}$BC,
∴△PEF∽△PBC,
∴$\frac{EF}{BC}$=$\frac{1}{2}$,
∴$\frac{{S}_{△PEF}}{{S}_{△PBC}}$=$\frac{1}{4}$,
∵S△PEF=2,
∴S△PBC=8,
∵四边形ABCD是平行四边形,
∴S?ABCD=2×8=16.
故答案为:16.
点评 此题主要考查了平行四边形的性质以及相似三角形的判定与性质以及三角形中位线定理等知识,得出$\frac{{S}_{△PEF}}{{S}_{△PBC}}$=$\frac{1}{4}$是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{30}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
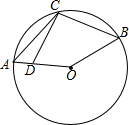 如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )
如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )| A. | ∠DCB+$\frac{1}{2}$∠O=180° | B. | ∠ACB+$\frac{1}{2}$∠O=180° | C. | ∠ACB+∠O=180° | D. | ∠CAO+∠CBO=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
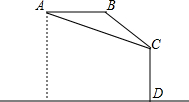 如图,热气球在离地面800米的A处,在A处测得一大楼顶C的俯角是30°,热气球沿着水平方向向此大楼飞行400米后达到B处,从B处再次测得此大楼楼顶C的俯角是45°,求该大楼CD的高度.
如图,热气球在离地面800米的A处,在A处测得一大楼顶C的俯角是30°,热气球沿着水平方向向此大楼飞行400米后达到B处,从B处再次测得此大楼楼顶C的俯角是45°,求该大楼CD的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com