
【题目】已知关于x的二次函数y=ax2+bx+c的图象经过点(﹣2,y1),(﹣1,y2),(1,0),且y1<0<y2 , 对于以下结论:
①abc>0;②a+3b+2c≤0;③对于自变量x的任意一个取值,都有 ![]() x2+x≥﹣
x2+x≥﹣ ![]() ;④在﹣2<x<﹣1中存在一个实数x0 , 使得x0=﹣
;④在﹣2<x<﹣1中存在一个实数x0 , 使得x0=﹣ ![]() ,
,
其中结论错误的是 (只填写序号).
【答案】②
【解析】解:由题意二次函数图象如图所示,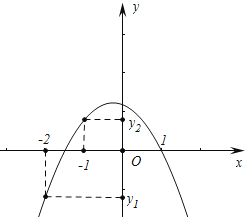
∴a<0.b<0,c>0,
∴abc>0,故①正确.
∵a+b+c=0,
∴c=﹣a﹣b,
∴a+3b+2c=a+3b﹣2a﹣2b=b﹣a,
又∵x=﹣1时,y>0,
∴a﹣b+c>0,
∴b﹣a<c,
∵c>O,
∴b﹣a可以是正数,
∴a+3b+2c≤0,故②错误.
所以答案是②.
∵函数y′= ![]() x2+x=
x2+x= ![]() (x2+
(x2+ ![]() x)=
x)= ![]() (x+
(x+ ![]() )2﹣
)2﹣ ![]() ,∵
,∵ ![]() >0,∴函数y′有最小值﹣
>0,∴函数y′有最小值﹣ ![]() ,∴
,∴ ![]() x2+x≥﹣
x2+x≥﹣ ![]() ,故③正确.
,故③正确.
∵y=ax2+bx+c的图象经过点(1,0),
∴a+b+c=0,
∴c=﹣a﹣b,
令y=0则ax2+bx﹣a﹣b=0,设它的两个根为x1 , 1,
∵x11= ![]() =﹣
=﹣ ![]() ,∴x1=﹣
,∴x1=﹣ ![]() ,
,
∵﹣2<x1<x2 ,
∴在﹣2<x<﹣1中存在一个实数x0 , 使得x0=﹣ ![]() ,故④正确,
,故④正确,
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
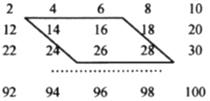
【题目】如图所示的数阵是由50个偶数排成的.
(1)图中框内的4个数有什么关系?
(2)在数阵图中任意作一类似于(1)中的框,设其中的一个数为![]() ,那么其他三个数怎样表示?
,那么其他三个数怎样表示?
(3)如果四个数的和是172,能否求出这4个数?
(4)如果四个数的和是322,能否求出这4个数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC 中,AB=AC,∠BAC=90°,D 是BC 上一点,EC⊥BC,EC=BD,DF=FE.
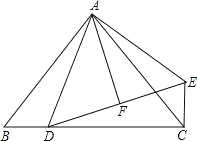
求证:(1)△ABD≌△ACE;
(2)AF⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究
问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为 .
拓展
问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.
推广
问题3 如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地,已知这列货车挂有A、B两种不同规格的货车车厢共40节,使用A型车厢每节费用为6000元,使用B型车厢每节费用为8000元。
(1)设运送这批货物的总费用为![]() 万元,这列货车挂A型车厢
万元,这列货车挂A型车厢![]() 节,试写出
节,试写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨,每节B型车厢最多可装甲种货物25吨和乙种货物35吨,装货时按此要求安排A、B两种车厢的节数,那么共有哪几种安排车厢的方案?
(3)在上述方案中,哪种方案运费最省,最少运费为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(x﹣3)(x﹣2)﹣p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1 , x2 , 且满足 ![]() ,求实数p的值.
,求实数p的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com