
【题目】已知:∠AOB= ![]() °,过点O作OB⊥OC.请画图示意并求解.
°,过点O作OB⊥OC.请画图示意并求解.
(1)若 ![]() =30,则∠AOC=.
=30,则∠AOC=.
(2)若 ![]() =40,射线OE平分∠AOC , 射线OF平分∠BOC , 求∠EOF的度数;
=40,射线OE平分∠AOC , 射线OF平分∠BOC , 求∠EOF的度数;
(3)若0< ![]() <180,射线OE平分∠AOC , 射线OF平分∠BOC , 则∠EOF=°.(用
<180,射线OE平分∠AOC , 射线OF平分∠BOC , 则∠EOF=°.(用 ![]() 的代数式表示).
的代数式表示).
【答案】
(1)120°或60°
(2)解:示意图画出,20°;
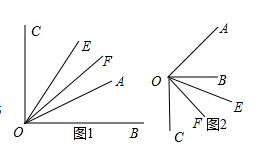
当射线OA,OC在射线OB同侧时,
∵OE平分∠AOC,OF平分∠BOC,
∴∠COE=![]() ∠AOC,∠COF=
∠AOC,∠COF=![]() ∠BOC,
∠BOC,
∴∠EOF=∠COF-∠COE=![]() (∠BOC-∠AOC)=
(∠BOC-∠AOC)=![]() (90°-90°+40°)=20°;
(90°-90°+40°)=20°;
当射线OA,OC在射线OB两侧时,
∠EOF=∠COF-∠COE=![]() (∠BOC-∠AOC)=
(∠BOC-∠AOC)=![]() (90°+40°-90°)=20°,
(90°+40°-90°)=20°,
故∠EOF为20°;
(3)![]()
![]()
【解析】解:(1)∵OB⊥OC,
∴∠BOC=90°,
当射线OA,OC在射线OB同侧时,∠AOC=∠AOB-∠BOC=60°,
当射线OA,OC在射线OB两侧时,∠AOC=∠AOB+∠BOC=120°;
所以答案是:120°或60°;
(3)当射线OA,OC在射线OB同侧时,
∵OE平分∠AOC,OF平分∠BOC,
∴∠COE=![]() ∠AOC,∠COF=
∠AOC,∠COF=![]() ∠BOC,
∠BOC,
∴∠EOF=∠COF-∠COE=![]() (∠BOC-∠AOC)=
(∠BOC-∠AOC)=![]() (90°-90°+
(90°-90°+![]() )=
)=![]() °;
°;
当射线OA,OC在射线OB两侧时,
∠EOF=∠COF-∠COE=![]() (∠BOC-∠AOC)=
(∠BOC-∠AOC)=![]() (90°+
(90°+![]() -90°)=
-90°)=![]() .
.
所以答案是:![]() .
.
(1)分射线OA,OC在射线OB同侧和两侧来讨论求解;
(2)分射线OA,OC在射线OB同侧和两侧来讨论,再由角平分线的定义来求解;
(3)与(2)解法相同.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对角的运算的理解,了解角之间可以进行加减运算;一个角可以用其他角的和或差来表示.


科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和BC′F的周长之和为( ) 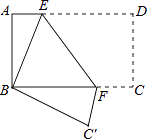
A.3
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O在线段AB上,点C,D分别是AO,BO的中点![]()
(1)AO=CO;BO=DO;
(2)若CO=3cm,DO=2cm,求线段AB的长度;
(3)若线段AB=10,小明很轻松地求得CD=5.他在反思过程中突发奇想:若点O在线段AB的延长线上,原有的结论“CD=5”是否仍然成立呢?请帮小明画出图形分析,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邻补角是指( )
A. 和为180°的两个角 B. 有一条公共边且相等的两个角
C. 有公共顶点且互补的两个角 D. 有公共顶点且有一条公共边,另一边互为反向延长线的两个角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com