
【题目】如图,已知点O在线段AB上,点C,D分别是AO,BO的中点![]()
(1)AO=CO;BO=DO;
(2)若CO=3cm,DO=2cm,求线段AB的长度;
(3)若线段AB=10,小明很轻松地求得CD=5.他在反思过程中突发奇想:若点O在线段AB的延长线上,原有的结论“CD=5”是否仍然成立呢?请帮小明画出图形分析,并说明理由.
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠ACB=90°,BC=3,AC=4,在直线BC上找一点P,使得△ABP为以AB为腰的等腰三角形,则PC的长度为 . 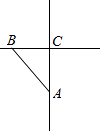
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且 OM恰好平分∠BOC.此时∠AOM=度;
(2)如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )
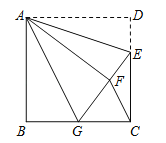
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB= ![]() °,过点O作OB⊥OC.请画图示意并求解.
°,过点O作OB⊥OC.请画图示意并求解.
(1)若 ![]() =30,则∠AOC=.
=30,则∠AOC=.
(2)若 ![]() =40,射线OE平分∠AOC , 射线OF平分∠BOC , 求∠EOF的度数;
=40,射线OE平分∠AOC , 射线OF平分∠BOC , 求∠EOF的度数;
(3)若0< ![]() <180,射线OE平分∠AOC , 射线OF平分∠BOC , 则∠EOF=°.(用
<180,射线OE平分∠AOC , 射线OF平分∠BOC , 则∠EOF=°.(用 ![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个小球从点A(3,3)出发,经过y轴上点C反弹后经过点B(1,0),则小球从A点经过点C到B点经过的最短路线长是( )
A.4
B.5
C.6
D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com