

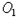 、
、
 外切于点T,经过点T的任一直线分别与
外切于点T,经过点T的任一直线分别与
 、
、
 交于点A、B,
交于点A、B,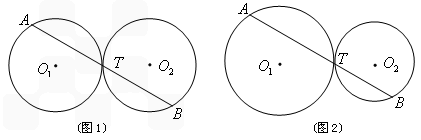

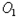 、
、
 是等圆(如图1),求证AT=BT;
是等圆(如图1),求证AT=BT;
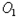 、
、
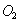 的半径分别为R、r(如图2),试写出线段AT、BT与R、r之间始终存在的数量关系(不需要证明)。
的半径分别为R、r(如图2),试写出线段AT、BT与R、r之间始终存在的数量关系(不需要证明)。 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源:素质教育新学案·初中几何·第三册 题型:047
如图所示,已知⊙![]() 与⊙
与⊙![]() 外切于F点,DE为公切线,过F点的直线交⊙
外切于F点,DE为公切线,过F点的直线交⊙![]() 于点A,交⊙
于点A,交⊙![]() 于点B,BE、AD的延长线交于C点,求证AC⊥BC.
于点B,BE、AD的延长线交于C点,求证AC⊥BC.

查看答案和解析>>
科目:初中数学 来源: 题型:044
(2005武汉)如图,已知: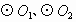 外切于点P,A是
外切于点P,A是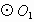 上一点,直线AC切
上一点,直线AC切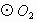 于点C交
于点C交 于点B,直线AP交⊙
于点B,直线AP交⊙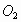 于点D.
于点D.
|
|
|
(1)请你判断∠BPC=∠CPD是否成立(不需证明);
(2)将“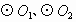 外切于点P”改为“
外切于点P”改为“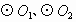 内切于点P”,其他条件不变.(1)中的结论是否仍然成立?画出图形并证明你的结论.
内切于点P”,其他条件不变.(1)中的结论是否仍然成立?画出图形并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2012届上海市嘉定宝山九年级二模数学试卷(带解析) 题型:解答题
已知⊙ 、⊙
、⊙ 外切于点
外切于点 ,经过点
,经过点 的任一直线分别与⊙
的任一直线分别与⊙ 、⊙
、⊙ 交于点
交于点 、
、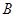 ,
,
(1)若⊙ 、⊙
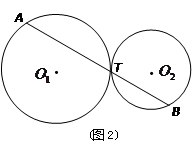
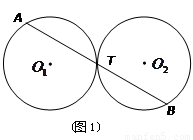
、⊙ 是等圆(如图1),求证
是等圆(如图1),求证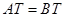 ;
;
(2)若⊙ 、⊙
、⊙ 的半径分别为
的半径分别为 、
、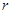 (如图2),试写出线段
(如图2),试写出线段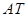 、
、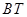 与
与 、
、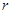 之间始终存在的数量关系(不需要证明).
之间始终存在的数量关系(不需要证明).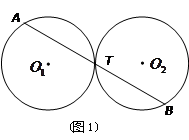
查看答案和解析>>
科目:初中数学 来源:2011-2012学年上海市嘉定宝山九年级二模数学试卷(解析版) 题型:解答题
已知⊙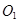 、⊙
、⊙ 外切于点
外切于点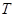 ,经过点
,经过点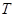 的任一直线分别与⊙
的任一直线分别与⊙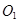 、⊙
、⊙ 交于点
交于点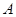 、
、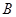 ,
,
(1)若⊙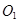 、⊙
、⊙ 是等圆(如图1),求证
是等圆(如图1),求证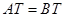 ;
;
(2)若⊙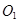 、⊙
、⊙ 的半径分别为
的半径分别为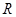 、
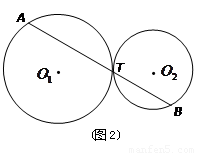
、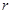 (如图2),试写出线段
(如图2),试写出线段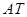 、
、 与
与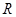 、
、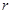 之间始终存在的数量关系(不需要证明).
之间始终存在的数量关系(不需要证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com