
【题目】我校初三某班 50 名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计表如表所示:
自选项目 | 人数 | 频率 |
立定跳远 | 9 | 0.18 |
三级蛙跳 | 12 | a |
一分钟跳绳 | 8 | 0.16 |
投掷实心球 | b | 0.32 |
推铅球 | 5 | 0.10 |
合计 | 50 | 1 |
(1)填空:a= ,b= ;
(2)若将各自选项目的人数所占比例绘制成扇形统计图,求“立定跳远”对应扇形的圆心角的度数;
(3)在选报“推铅球”的学生中,有 3 名男生、2 名女生,为了了解学生的训练效果,从这 5 名学生中随机抽取两名学生进行推铅球测试,请用列表法或树形图法求所抽取的两名学生中至多有一名男生的概率.
【答案】(1)0.24、16;(2)64.8°;(3)所抽取的两名学生中至多有一名男生的概率为![]() .
.
【解析】分析: (1)根据表格求出a与b的值即可;
(2)用360°乘以“立定跳远”对应的频率即可得;
(3)画树状图得出所有等可能的情况数,找出抽取的两名学生中至多有一名男生的情况,即可求出所求概率.
详解:
(1)a=12÷50=0.24,b=50×0.32=16,
故答案为:0.24、16;
(2)若将各自选项目的人数所占比例绘制成扇形统计图,则“立定跳远”对应扇形的圆心角的度数为360°×0.18=64.8°;
(3)画树状图为:

共有20种等可能的结果数,其中所抽取的两名学生中至多有一名男生的结果数为14,
所以所抽取的两名学生中至多有一名男生的概率=![]() =
=![]() .
.
点睛: 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了统计图.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两名运动员进行长跑训练,两人距终点的路程![]() (米)与跑步时间
(米)与跑步时间![]() (分)之间的函数关系如图所示,根据图象所提供的信息解答问题:
(分)之间的函数关系如图所示,根据图象所提供的信息解答问题:
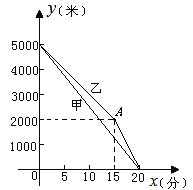
(1)他们在进行 米的长跑训练,在0<![]() <15的时间内,速度较快的人是 (填“甲”或“乙”);
<15的时间内,速度较快的人是 (填“甲”或“乙”);
(2)求乙距终点的路程![]() (米)与跑步时间
(米)与跑步时间![]() (分)之间的函数关系式;
(分)之间的函数关系式;
(3)当![]() =15时,两人相距多少米?
=15时,两人相距多少米?
(4)在15<![]() <20的时间段内,求两人速度之差.
<20的时间段内,求两人速度之差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示的数a、点B表示数b,a、b满足|a﹣30|+(b+6)2=0.点O是数轴原点.
![]()
(1)点A表示的数为 ,点B表示的数为 ,线段AB的长为 .
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=2BC,则点C在数轴上表示的数为 .
(3)现有动点P、Q都从B点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到O点时,点Q才从B点出发,并以每秒3个单位长度的速度向右移动,且当点P到达A点时,点Q就停止移动,设点P移动的时间为t秒,问:当t为多少时,P、Q两点相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
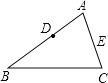
【题目】如图,在△ABC中,AB=6,AC=8,D是AB的中点.若在AC上存在一点E,使得△ADE与原三角形相似.
(1)确定E的位置,并画出简图:
(2)求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛自古就是中国的!2017年5月18日,中国海警2305,2308,2166,33115舰船队在中国的钓鱼岛领海内巡航,如图,我军以30km/h的速度在钓鱼岛A附近进行合法巡逻,当巡逻舰行驶到B处时,战士发现A在他的东北方向,巡逻舰继续向北航行40分钟后到达点C,发现A在他的东偏北15°方向,求此时巡逻舰与钓鱼岛的距离(![]() ≈1.414,结果精确到0.01)
≈1.414,结果精确到0.01)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的不等式组![]() 的整数解仅有1,2,那么适合这个不等式组的整数a,b组成的有序数对(a,b)共有( )
的整数解仅有1,2,那么适合这个不等式组的整数a,b组成的有序数对(a,b)共有( )
A. 2个B. 4个C. 6个D. 8个
查看答案和解析>>
科目:初中数学 来源: 题型:
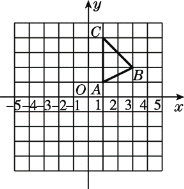
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,1),B(3,2),C(1,4).
(1)将△ABC先向下平移4个单位,再向右平移1个单位,画出第二次平移后的△A1B1C1.若将△A1B1C1看成是△ABC经过一次平移得到的,则平移距离是________.
(2)以原点为对称中心,画出与△ABC成中心对称的△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
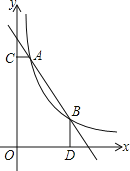
【题目】如图,一次函数![]() 与函数
与函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,
两点,![]() 轴于C,
轴于C,![]() 轴于D
轴于D
![]() 求k的值;
求k的值;
![]() 根据图象直接写出
根据图象直接写出![]() 的x的取值范围;
的x的取值范围;
![]() 是线段AB上的一点,连接PC,PD,若
是线段AB上的一点,连接PC,PD,若![]() 和
和![]() 面积相等,求点P坐标.
面积相等,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;

(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com