
【题目】如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;

(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
【答案】(1)抛物线的解析式为y=﹣x2+3x+4.(2)点P的坐标为(2,6)或(4,0).(3)△PBC的面积的最大值为8.
【解析】试题分析:(1)将点A(-1,0),B(4,0)的坐标代入抛物线的解析式,求得b、c的值即可;
(2)先由函数解析式求得点C的坐标,从而得到△OBC为等腰直角三角形,故此当CF=PF时,以P,C,F为顶点的三角形与△OBC相似.
设点P的坐标为(a,-a2+3a+4).则CF=a,PF=-a2+3a,接下来列出关于a的方程,从而可求得a的值,于是可求得点P的坐标;
(3)连接EC.设点P的坐标为(a,-a2+3a+4).则OE=a,PE=-a2+3a+4,EB=4-a.然后依据S△PBC=S四边形PCEB-S△CEB列出△PBC的面积与a的函数关系式,从而可求得三角形的最大面积.
试题解析:(1)将点A(-1,0),B(4,0)的坐标代入函数的表达式得:
![]() ,
,
解得:b=3,c=4.
抛物线的解析式为y=-x2+3x+4.
(2)如图1所示:
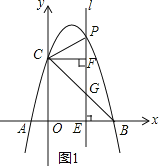
∵令x=0得y=4,
∴OC=4.
∴OC=OB.
∵∠CFP=∠COB=90°,
∴FC=PF时,以P,C,F为顶点的三角形与△OBC相似.
设点P的坐标为(a,-a2+3a+4)(a>0).
则CF=a,PF=|-a2+3a+4-4|=|a2-3a|.
∴|a2-3a|=a.
解得:a=2,a=4.
∴点P的坐标为(2,6)或(4,0).
(3)如图2所示:连接EC.
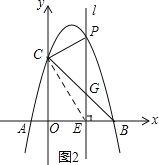
设点P的坐标为(a,-a2+3a+4).则OE=a,PE=-a2+3a+4,EB=4-a.
∵S四边形PCEB=![]() OBPE=
OBPE=![]() ×4(-a2+3a+4),S△CEB=
×4(-a2+3a+4),S△CEB=![]() EBOC=
EBOC=![]() ×4×(4-a),
×4×(4-a),
∴S△PBC=S四边形PCEB-S△CEB=2(-a2+3a+4)-2(4-a)=-2a2+8a.
∵a=-2<0,
∴当a=2时,△PBC的面积S有最大值.
∴P(2,6),△PBC的面积的最大值为8.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c与直线y=﹣x+6分别交于x轴和y轴上同一点,交点分别是点B和点C,且抛物线的对称轴为直线x=4.
(1)求出抛物线与x轴的两个交点A,B的坐标.
(2)试确定抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
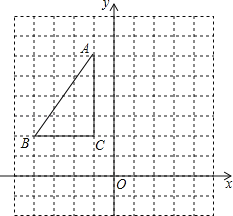
【题目】如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,6),B(﹣4,2),C(﹣1,2)
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC绕点B顺时针旋转90°后得到△A2BC2,请画出△A2BC2,并求出线段AB在旋转过程中扫过的图形面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
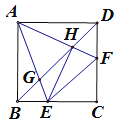
【题目】如图,正方形ABCD中,点E、F分别是BC、CD上的动点(不与点B,C,D重合),且∠EAF=45°,AE、AF与对角线BD分别相交于点G、H,连接EH、EF,则下列结论:
① △ABH∽△GAH; ② △ABG∽△HEG; ③ AE=![]() AH; ④ EH⊥AF; ⑤ EF=BE+DF
AH; ④ EH⊥AF; ⑤ EF=BE+DF
其中正确的有( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1:已知△ABC中,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE、CD,请你完成图形(尺规作图,不写作法.但要保留作图痕迹).
(2)如图2,已知△ABC中,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE、CD,判断BE与CD有什么数量关系,并加以证明.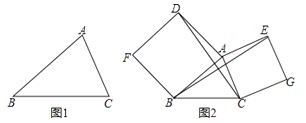
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com