
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②![]() >0;③ac﹣b+1=0;④OAOB=﹣
>0;③ac﹣b+1=0;④OAOB=﹣![]() .
.
其中正确结论的个数是( )

A.4 B.3 C.2 D.1
【答案】B
【解析】
试题分析:由抛物线开口方向得a<0,由抛物线的对称轴位置可得b>0,由抛物线与y轴的交点位置可得c>0,则可对①进行判断;根据抛物线与x轴的交点个数得到b2﹣4ac>0,加上a<0,则可对②进行判断;利用OA=OC可得到A(﹣c,0),再把A(﹣c,0)代入y=ax2+bx+c得ac2﹣bc+c=0,两边除以c则可对③进行判断;设A(x1,0),B(x2,0),则OA=﹣x1,OB=x2,根据抛物线与x轴的交点问题得到x1和x2是方程ax2+bx+c=0(a≠0)的两根,利用根与系数的关系得到x1x2=![]() ,于是OAOB=﹣
,于是OAOB=﹣![]() ,则可对④进行判断.
,则可对④进行判断.
解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴的右侧,
∴b>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①正确;
∵抛物线与x轴有2个交点,
∴△=b2﹣4ac>0,
而a<0,
∴![]() <0,所以②错误;
<0,所以②错误;
∵C(0,c),OA=OC,
∴A(﹣c,0),
把A(﹣c,0)代入y=ax2+bx+c得ac2﹣bc+c=0,
∴ac﹣b+1=0,所以③正确;
设A(x1,0),B(x2,0),
∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,
∴x1和x2是方程ax2+bx+c=0(a≠0)的两根,
∴x1x2=![]() ,
,
∴OAOB=﹣![]() ,所以④正确.
,所以④正确.
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中, AB =AC=24 cm, BC=16cm,AD= BD.如果点P在线段BC上以 2 cm/s 的速度由B点向C点运动,同时,点 Q在线段CA上以v cm/s 的速度由C点向A点运动,那么当△BPD 与△CQP全等时,v =( )
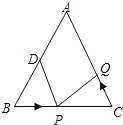
A.3B.4C.2或 4D.2或3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年4月23日是 “世界读书日”,宜宾市某中学举行“多读书,读好书”活动,对学生的课外读书时间进行了随机问卷调查,用调查结果绘制了图1、图2两幅统计图(均不完整),请根据统计图解答以下问题:
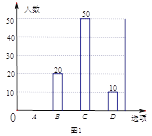
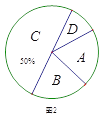
(1)本次接受问卷调查的学生共有________人,在扇形统计图中“D”选项所占的百分比为________;
(2)扇形统计图中,“B”选项所对应扇形圆心角为________度;
(3)请补全条形统计图;
(4)若该校共有1200名学生,则该校学生课外读书时间在“A”选项的约有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】泰勒斯是古希腊哲学家,相传他利用三角形全等的方法求出岸上一点到海中一艘船的距离.如图,B是观察点,船A在B的正前方,过B作AB的垂线,在垂线上截取任意长BD,C是BD的中点,观察者从点D沿垂直于BD的DE方向走,直到点E、船A和点C在一条直线上,那么△ABC≌△EDC,从而量出DE的距离即为船离岸的距离AB,这里判定△ABC≌△EDC的方法是( )

A.SASB.ASAC.AASD.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善小区环境,某小区决定要在一块边靠墙(墙长18m)的空地,修建一个矩形绿地ABCD,绿地一边靠墙,另三边用总长为40m的栅栏围住(如图),设AB边为xm,绿地面积为ym2.
(1)求y与x之间的函数关系,并求出自变量x的取值范围;
(2)绿地的面积能不能为200m2?如果能,求出x的值,如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、D都在⊙O上,过C点作CA∥BD,交OD的延长线于点A,连接BC,∠B=∠A=30,BD=![]() 。
。
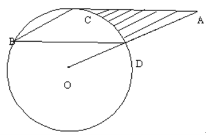
(1)求证:AC是⊙O的切线。
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积(结果保留π)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的爸爸开车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:
时刻 | 12:00 | 13:00 | 14:30 |
碑上的数 | 是一个两位数,数字之和是6 | 是一个两位数,十位与个位数字与12:00时所看到的正好颠倒了 | 比12:00时看到的两位数中间多了个0 |
则12:00时看到的两位数是多少?设12:00时看到的两位数的个位数为y,十位数为x,列出的二元一次方程组为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() 的图象交于A(a,-2),B两点.
的图象交于A(a,-2),B两点.
(1)求反比例函数的表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com