
 如图,菱形ABCD中,AB=4,∠ABC=60°,对称中心为P,点F为BC边上一个动点,点E在AB边上,且满足条件∠EPF=60°,图中两块阴影部分图形关于直线AC成轴对称,设它们的面积和为S1.
如图,菱形ABCD中,AB=4,∠ABC=60°,对称中心为P,点F为BC边上一个动点,点E在AB边上,且满足条件∠EPF=60°,图中两块阴影部分图形关于直线AC成轴对称,设它们的面积和为S1.分析 (1)如图1中,相似.只要证明∠4=∠5=60°,∠1=∠3即可证明.
(2)①如图2中,作PG⊥AB于G,PH⊥BC于H,连接PB.由△PAE∽△FCP,得$\frac{CF}{AP}$=$\frac{CP}{AE}$,得$\frac{x}{2}$=$\frac{2}{AE}$,推出AE=$\frac{4}{x}$,BE=4-$\frac{4}{x}$,由此即可解决问题.
②如图3中,只要证明△PCF是等边三角形,即可推出x=2,利用①的结论即可解决问题.
解答 解:(1)如图1中,相似.理由如下: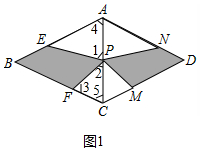
∵四边形ABCD是菱形,∠ABC=60°,
∴AB=BC=AD=CD,∠ABC=∠ADC=60°,
∴△ABC,△ADC都是等边三角形,
∴∠4=∠5=60°,
∵∠EPF=60°,
∴∠1+∠2=120,∠2+∠3=120°,
∴∠1=∠3,
∴△PAE∽△FCP.
(2)②如图2中,作PG⊥AB于G,PH⊥BC于H,连接PB.
∵BA=BC,AP=PC,
∴∠PBA=∠PBC,
∵PG⊥AB,PH⊥BC,
∴PG=PH,
∵△PAE∽△FCP,
∴$\frac{CF}{AP}$=$\frac{CP}{AE}$,
∴$\frac{x}{2}$=$\frac{2}{AE}$,
∴AE=$\frac{4}{x}$,
∴BE=4-$\frac{4}{x}$,
∴y=$\frac{2•(4-\frac{4}{x}+4-x)•PG}{2•x•PH}$=$\frac{8}{x}$-$\frac{4}{{x}^{2}}$-1(1≤x≤4).
③如图3中,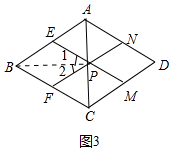
∵图中两块阴影部分图形关于点P成中心对称,
∴∠APE=∠APN=∠CPF=∠CPM,
∵∠EPF=∠MPN=60°,
∴∠APE=∠CPF=60°,
∴∠1=∠2=30°,∠C=∠CPF=60°,
∴△PCF是等边三角形,
∴CF=CP=x=2,
∴y=$\frac{8}{2}$-$\frac{4}{{2}^{2}}$-1=2.
点评 本题考查相似形综合题、菱形的性质、等边三角形的性质等知识,解题的关键是熟练应用这些知识解决问题,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,A(-2,0),B(8,0),以AB为直径作半圆P交y轴于点D,过点B作BC⊥x轴,且BC=10,连结CD.
如图,平面直角坐标系中,A(-2,0),B(8,0),以AB为直径作半圆P交y轴于点D,过点B作BC⊥x轴,且BC=10,连结CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某农场拟建三件矩形饲养室,饲养室一面靠现有墙(墙可用长≤20m),中间用两道墙隔开,已知计划中的建筑材料可建围墙的总长为60m,设饲养室宽为x(m),总占地面积为y(m2)(如图所示).
某农场拟建三件矩形饲养室,饲养室一面靠现有墙(墙可用长≤20m),中间用两道墙隔开,已知计划中的建筑材料可建围墙的总长为60m,设饲养室宽为x(m),总占地面积为y(m2)(如图所示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com