
 某农场拟建三件矩形饲养室,饲养室一面靠现有墙(墙可用长≤20m),中间用两道墙隔开,已知计划中的建筑材料可建围墙的总长为60m,设饲养室宽为x(m),总占地面积为y(m2)(如图所示).
某农场拟建三件矩形饲养室,饲养室一面靠现有墙(墙可用长≤20m),中间用两道墙隔开,已知计划中的建筑材料可建围墙的总长为60m,设饲养室宽为x(m),总占地面积为y(m2)(如图所示).分析 (1)设饲养室宽为x(m),则长为(60-4x)m,根据长方形面积公式即可得,由墙可用长≤20m可得x的范围;
(2)令y=210求出x,根据(1)中x的范围即可判断.
解答 解:(1)设饲养室宽为x(m),则长为(60-4x)m,
∴y=x(60-4x)=-4x2+60x,
∵0<60-4x≤20,
∴10≤x<15;
(2)不能,理由如下:
当y=210时,-4x2+60x=210,
解得:x=$\frac{15+\sqrt{15}}{2}$或x=$\frac{15-\sqrt{15}}{2}$,
∵x=$\frac{15+\sqrt{15}}{2}$<10,且x=$\frac{15-\sqrt{15}}{2}$<10,
∴不能.
点评 本题主要考查二次函数的应用,解题的关键是将实际问题转化为数学问题以后,准确列出二次函数关系式,正确运用二次函数的有关性质来解题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
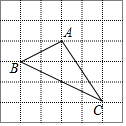 如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点A、B、C为顶点的三角形的面积是4,周长是3$\sqrt{5}$+$\sqrt{13}$.
如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点A、B、C为顶点的三角形的面积是4,周长是3$\sqrt{5}$+$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,菱形ABCD中,AB=4,∠ABC=60°,对称中心为P,点F为BC边上一个动点,点E在AB边上,且满足条件∠EPF=60°,图中两块阴影部分图形关于直线AC成轴对称,设它们的面积和为S1.
如图,菱形ABCD中,AB=4,∠ABC=60°,对称中心为P,点F为BC边上一个动点,点E在AB边上,且满足条件∠EPF=60°,图中两块阴影部分图形关于直线AC成轴对称,设它们的面积和为S1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com