
如图,在直角梯形OABC中,OA、OC边所在直线与x、y轴重合,BC∥OA,点B的坐标为(6. 4,4. 8),对角线OB⊥OA.在线段OA、AB上有动点E、D,点E以每秒2厘米的速度在线段OA上从点O向点A匀速运动,同时点D以每秒1厘米的速度在线段AB上从点A向点B匀速运动.当点E到达点A时,点D同时停止运动.设点E的运动时间为t(秒),
(1)求线段AB所在直线的解析式;
(2)设四边形OEDB的面积为y,求y关于t的函数关系式,并写出自变量的t的取值范围;
(3)在运动过程中,存不存在某个时刻,使得以A、E、D为顶点的三角形与△ABO相似,若存在求出这个时刻t,若不存在,说明理由.

(1)过点B作BH⊥OA,垂足为点H
∵∠COA=90°.BC∥OA∴∠BCO=90°
∴四边形COHB是矩形∴BH=CO,BC=OH
∵B(6. 4,4. 8)∴OH=6. 4,BH=4. 8
∴![]() ………………………………………………………………2分
………………………………………………………………2分
∵OB⊥BA∴∠OBA=90°
 ∴∠OBA=∠OHB=90°
∴∠OBA=∠OHB=90°
∵∠BOH=∠AOB
∴△BOH∽△BOA
∴![]()
∴OB2=AO·OH
∴82=OA·6. 4,OA=10 …………………………………………………………3分
∴AB=![]()
∴A(10,0),设直线AB的解析式为![]()
![]() 解得k=
解得k=![]() ,
,![]()
∴![]() ……………………………………………………………………4分
……………………………………………………………………4分
(2)过点D作DF⊥OA,垂足为F.
∴DF∥BH
∴△ADF∽△ABH
∴![]() ,
,![]() ,DF=0. 8 ……………………………………………5分
,DF=0. 8 ……………………………………………5分
∵OE=2t,AE=10-2t
![]()
∴![]() (0<t≤5)………………………………………………………7分
(0<t≤5)………………………………………………………7分
(3)①∠ADE=90°∠BAO=∠DAE
当![]() 时,△ADE∽△ABO
时,△ADE∽△ABO
![]() 解得
解得![]() ………………………………………………………………9分
………………………………………………………………9分
②∠AED=90°∵∠OAB=∠DAE
当![]() 时△AED∽△ABO
时△AED∽△ABO
∴![]() 解得
解得![]() ……………………………………………………10分
……………………………………………………10分
∴当![]() 或
或![]() 秒时,以A、E、D为顶点的三角形与△ABO相似………11分
秒时,以A、E、D为顶点的三角形与△ABO相似………11分
【相关知识点】三角形相似,一次函数、二次函数,一元一次方程
【解题思路】将动点静止在某一时刻,转化为相关三角形的知识求解.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
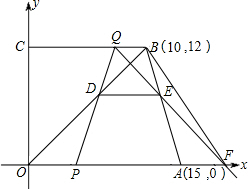 动时间为t(单位:秒).
动时间为t(单位:秒).查看答案和解析>>
科目:初中数学 来源: 题型:
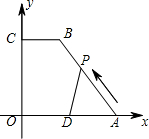 (10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
(10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 单位,移动时间记为t秒.
单位,移动时间记为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,2),C(3,0).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ⊥直线OA,垂足为Q.设P点移动的时间为t秒(0<t≤7),△OPQ与直角梯形OABC重叠部分的面积为S.
如图,在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,2),C(3,0).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ⊥直线OA,垂足为Q.设P点移动的时间为t秒(0<t≤7),△OPQ与直角梯形OABC重叠部分的面积为S.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com