
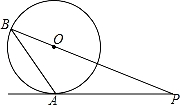
如图,PA是⊙O的切线,切点为A,PO的延长线交⊙O于点B.若∠ABP=33°,则∠P= °.
 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
用配方法解一元二次方程x2﹣6x﹣10=0时,下列变形正确的为( )
A.(x+3)2=1 B.(x﹣3)2=1 C.(x+3)2=19 D.(x﹣3)2=19
查看答案和解析>>
科目:初中数学 来源: 题型:
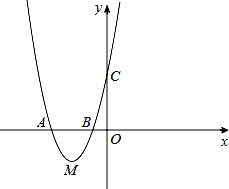
如图,抛物线经过A(﹣2,0),B(﹣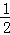 ,0),C(0,2)三点.
,0),C(0,2)三点.
(1)求抛物线的解析式;
(2)在直线AC下方的抛物线上有一点D,使得△DCA的面积最大,求点D的坐标;
(3)设点M是抛物线的顶点,试判断抛物线上是否存在点H满足∠AMH=90°?若存在,请求出点H的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com