
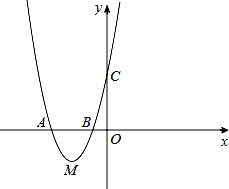
如图,抛物线经过A(﹣2,0),B(﹣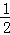 ,0),C(0,2)三点.
,0),C(0,2)三点.
(1)求抛物线的解析式;
(2)在直线AC下方的抛物线上有一点D,使得△DCA的面积最大,求点D的坐标;
(3)设点M是抛物线的顶点,试判断抛物线上是否存在点H满足∠AMH=90°?若存在,请求出点H的坐标;若不存在,请说明理由.
【考点】二次函数综合题.
【专题】压轴题.
【分析】(1)根据待定系数法,可得抛物线的解析式;
(2)根据图形的割补法,可得面积的和差,根据二次函数的性质,可得答案;
(3)根据余角的性质,可得∠AMN=∠NKM,根据相似三角形的判定与性质,可得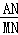 =
=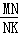 ,根据解方程组,可得H点坐标.
,根据解方程组,可得H点坐标.
【解答】解:(1)设抛物线的解析式为y=ax2+bx+c,将A(﹣2,0),B(﹣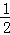 ,0),C(0,2)代入解析式,得
,0),C(0,2)代入解析式,得
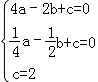 ,
,
解得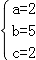 .
.
∴抛物线的解析式是y=2x2+5x+2;
(2)由题意可求得AC的解析式为y=x+2,
如图1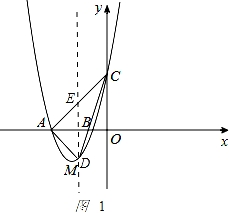 ,
,
设D点的坐标为(t,2t2+5t+2),过D作DE⊥x轴交AC于E点,
∴E点的坐标为(t,t+2),
DE=t+2﹣(2t2+5t+2)=﹣2t2﹣4t,用h表示点C到线段DE所在直线的距离,
S△DAC=S△CDE+S△ADE=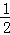 DE•h+
DE•h+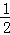 DE(2﹣h)=
DE(2﹣h)=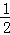 DE•2=DE=﹣2t2﹣4t=﹣2(t+1)2+2
DE•2=DE=﹣2t2﹣4t=﹣2(t+1)2+2
∵﹣2<t<0,
∴当t=﹣1时,△DCA的面积最大,此时D点的坐标为(﹣1,﹣1);
(3)存在点H满足∠AMH=90°,
由(1)知M点的坐标为(﹣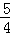 ,﹣
,﹣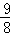 )
)
如图2:作MH⊥AM交x轴于点K(x,0),作MN⊥x轴于点N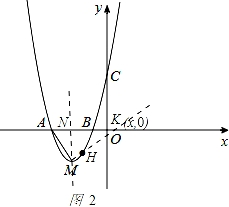 ,
,
∵∠AMN+∠KMA=90°,∠NKM+∠KMN=90°,
∴∠AMN=∠NKM.
∵∠ANM=∠MNK,
∴△AMN∽△MKN,
∴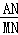 =
=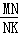 ,
,
∴MN2=AN•NK,
∴(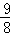 )2=(2﹣
)2=(2﹣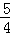 )(x+
)(x+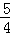 ),
),
解得x=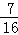
∴K点坐标为(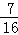 ,0)
,0)
直线MK的解析式为y= x﹣
x﹣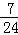 ,
,
∴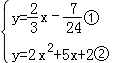 ,
,
把①代入②,化简得48x2+104x+55=0.
△=1042﹣4×48×55=64×4=256>0,
∴x1=﹣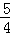 ,x2=﹣
,x2=﹣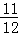 ,将x2=﹣
,将x2=﹣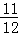 代入y=
代入y= x﹣
x﹣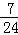 ,
,
解得y=﹣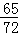
∴直线MN与抛物线有两个交点M、H,
∴抛物线上存在点H,满足∠AMH=90°,
此时点H的坐标为(﹣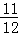 ,﹣
,﹣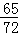 ).
).
【点评】本题考察了二次函数综合题,(1)利用待定系数法求函数解析式;(2)利用图形割补法求面积是解题关键,(3)利用相似三角形的判定与性质得出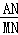 =
=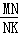 是解题关键,解方程组是此题的难点.
是解题关键,解方程组是此题的难点.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
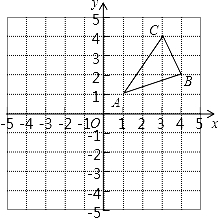
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
直线AB: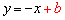 分别与x,y轴交于A ,B两点,点A的坐标为 (3,0),过点B的直线交x轴负半轴于点C,且OB:OC=3:1.
分别与x,y轴交于A ,B两点,点A的坐标为 (3,0),过点B的直线交x轴负半轴于点C,且OB:OC=3:1.
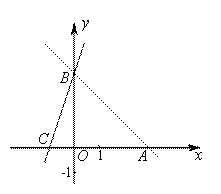 (1)求点B的坐标及直线BC的解析式;
(1)求点B的坐标及直线BC的解析式;
(2)在x轴上方存在点D,使以点A,B,D为顶点的
三角形与△ABC全等,画出△ABD并请直接写出点D的坐标;
(3)在线段OB上存在点P,使点P到点B,C的距离相等,
求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
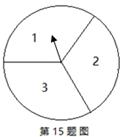
把一个转盘平均分成三等份,依次标上数字1、2、3,自由转动转盘两次,把第一次转动停止后指针指向的数字记做x,把第二次转动停止后指针指向的数字的2倍记作y,以长度分别为x,y,5的三条线段能构成三角形的概率为 ___________(长度单位一致)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com