练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
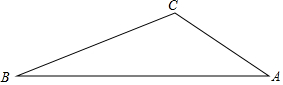
    19．如图，在△ABC中，∠B=30°，AC=2$\sqrt{3}$，BC=6，求sinA的值．

    分析 作高线CD，构建两个直角三角形，先根据30°角所对的直角边是斜边的一半求CD的长，所以在Rt△ACD中，利用三角函数的定义可得结论．

    解答 解：过C作CD⊥AB，垂足为D，
    在Rt△BCD中，∵∠B=30°，BC=6，
    ∴CD=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3，
    在Rt△ACD中，∵AC=2$\sqrt{3}$，
    ∴sin∠A=$\frac{CD}{AC}$=$\frac{3}{2\sqrt{3}}$=$\frac{\sqrt{3}}{2}$．

    点评 本题是解直角三角形，熟练掌握三角函数的定义是关键，同时还运用了直角三角形中30°角的性质，本题属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    9．在-3与-2中，是方程x2-x-6=0的解的是x=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．已知方程x2-3x-7=0的两根分别是a，b．则a2+5a+8b=31．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

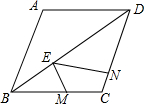    7．已知，如图，菱形ABCD中，∠ABC=60°，E为线段DB上的一点，∠MEN=60°，点M，N分别在直线BC，DC上．
    （1）如图1，当E再靠近B的三等分点上，求证：$\frac{1}{2}$DN+BM=BC；
    （2）如图2，当E再靠近D的三等分点上，点M在CB的延长线上时，点N在DC的延长线上时，则线段DN、BM、BC的数量关系为BC=DN+$\frac{1}{2}$BM．
    （3）在（2）的条件下，连接MN与AB，DB延长线交于F，G，若DN：CN=3：1，EM=8，求GF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，已知点A、B是数轴上的两点，O为原点，点B对应的数为3，AB=10．
    （1）填空：数轴上点A表示的数是-7；
    （2）动点P从O出发以每秒3个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）
    ①当动点P在线段AB上时，则AP=7-3t（用含t的代数式表示）；
    ②是否存在t值，使得BP=5AP成立？若存在，求出t的值；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．（1）|-3|+（-1）2011×（π-3）0-$\root{3}{27}$
    （2）|1-$\sqrt{2}$|-$\frac{1}{2}$$\sqrt{24}$-$\frac{2}{\sqrt{2}}$
    （3）解方程组$\left\{\begin{array}{l}{7x+3y-36=0}\\{2x+9y-51=0}\end{array}\right.$
    （4）解方程组$\left\{\begin{array}{l}{\frac{x}{3}-\frac{y}{4}=1}\\{3x-4y=2}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．某水果店的老板以单价为120元的价格购进一批进口高档水果，很快售完，老板又进行第二次购进，数量为第一次的两倍，但单价比第一次高出5元，两次购进共花了3700元．
    （1）第一批购这种进口高档水果多少千克？
    （2）老板以每件150元的价格销售第二批，售出80%后，为了尽快售完，决定打折促销，要使得第二批的销售利润不少于320元，剩余的水果每件售完至少打几折？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．某小区为改善居住环境，物业公司计划对面积为3000m2的区域进行绿化，安排甲、乙两个工程队完成．已知甲队每天能完成绿化的面积是乙队的1.5倍，如果要独立完成面积为3000m2区域的绿化，甲工程队比乙工程队可少用10天．
    （1）求甲、乙两工程队每天能完成绿化的面积分别是多少m2？
    （2）物业公司每天需付给甲队的绿化费用为0.5万元，需付给乙队的绿化费用为0.4万元，要使这次的绿化总费用不超过11.2万元，至少应安排甲队工作多少天？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．为提高饮水质量，越来越多的居民开始选购家用净水器，一商场抓住商机，从厂家购进了A、B、C三种型号家用净水器共n台，且购进B型号家用净水器的数量是A型号的2倍．已知A型号家用净水器进价是150元/台，B型号家用净水器进价是200元/台，C型号家用净水器进价是350元/台．若商家购买的总费用为70000元，求n的最大值？

    查看答案和解析>>

    同步练习册答案