
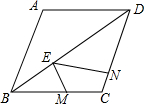
 已知,如图,菱形ABCD中,∠ABC=60°,E为线段DB上的一点,∠MEN=60°,点M,N分别在直线BC,DC上.
已知,如图,菱形ABCD中,∠ABC=60°,E为线段DB上的一点,∠MEN=60°,点M,N分别在直线BC,DC上.分析 (1)如图1中,连接AE、EC、AC,AC交BD于点O.首先证明△DEC是含有30°的直角三角形,由△EDN∽△ECM,推出$\frac{DN}{CM}$=$\frac{DE}{EC}$=$\frac{2}{1}$,推出CM=$\frac{1}{2}$DN,由此即可解决问题.
(2)如图2中,结论:BC=DN+$\frac{1}{2}$BM,证明方法类似(1).
(3)首先证明△EMN是直角三角形,BM=MC,由△BMF≌△CMN,推出BF=CN,FM=MN=4$\sqrt{3}$,由BF∥DN,得$\frac{FG}{GN}$=$\frac{BF}{DN}$,得$\frac{FG}{FG+8\sqrt{3}}$=$\frac{1}{3}$,即可求出GF.
解答 (1)证明:如图1中,连接AE、EC、AC,AC交BD于点O.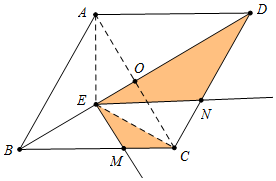
∵四边形ABCD是菱形,∠ABC=60°,
∴AB=BC,=CD=AD,∠ABC=∠ADC=60°,BD⊥AC,OB=OD,AO=OC,
∴△ABC,△ADC都是等边三角形,
∵BE=$\frac{1}{3}$BD,BO=OD,
∴BE=2EO,
∴点E是△ABC的重心,也是外接圆的圆心,
∴EB=EA=EC=2EO,∠ECO=∠ECB=30°,
∵∠ACD=60°,
∴∠ECD=90°,
∵∠EDC=30°,
∴DE=2EC,
∵∠DEC=∠MEN=60°,
∴∠DEN=∠MEC,
∵∠ECM=∠EDN,
∴△EDN∽△ECM,
∴$\frac{DN}{CM}$=$\frac{DE}{EC}$=$\frac{2}{1}$,
∴CM=$\frac{1}{2}$DN,
∴BC=BM+CM=BM+$\frac{1}{2}$DN.
(2)解:结论:BC=DN+$\frac{1}{2}$BM.理由如下:
如图2中,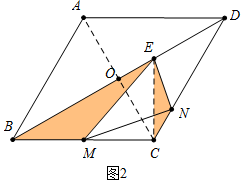
由(1)可知,△EBM∽△ECN,
∴$\frac{BM}{CN}$=$\frac{BE}{EC}$=2,
∴CN=$\frac{1}{2}$BM,
∴BC=CD=DN+CN=DN+$\frac{1}{2}$BM.
故答案为BC=DN+$\frac{1}{2}$BM.
(3)如图3中,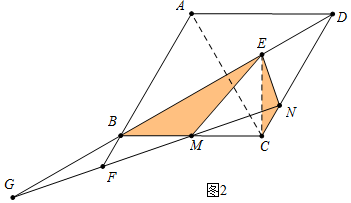
∵∠MEN+∠MCN=180°,
∴E、M、C、N四点共圆,
∴∠MNE=∠MCE=90°,
∵∠MEN=60°,
∴∠EMN=30°,
∴EM=2EN,∵EM=8,
∴EN=4,MN=4$\sqrt{3}$,设CN=a,则BM=2CN=2a,DN=3a,
∴CD=BC=4a,
∴BM=MC=2a,
∵BF∥CN,
∴∠BFM=∠MNC,
∵∠BMF=∠NMC,BM=CM,
∴△BMF≌△CMN,
∴BF=CN,FM=MN=4$\sqrt{3}$,
∵$\frac{FG}{GN}$=$\frac{BF}{DN}$,
∴$\frac{FG}{FG+8\sqrt{3}}$=$\frac{1}{3}$,
∴FG=4$\sqrt{3}$.
点评 本题考查四边形综合题、菱形的性质、等边三角形的性质、相似三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是正确寻找相似三角形,利用相似三角形的性质解决问题,第三个问题的关键是证明△EMN是直角三角形,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
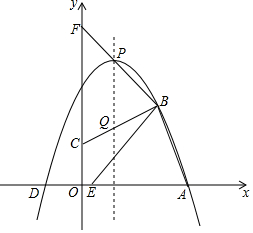 如图,二次函数y=ax2+bxc的图象经过A(4,0),D(-1,0)和B(3,3)三,.顶点为点P.作BC⊥BA交y轴于C,交对称轴于Q,将∠CBA绕点B顺时针旋转,∠CBA的两边分别交x轴、y轴于点E、F.设点E的坐标为(m,0).
如图,二次函数y=ax2+bxc的图象经过A(4,0),D(-1,0)和B(3,3)三,.顶点为点P.作BC⊥BA交y轴于C,交对称轴于Q,将∠CBA绕点B顺时针旋转,∠CBA的两边分别交x轴、y轴于点E、F.设点E的坐标为(m,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com