练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

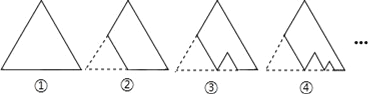
    【题目】图①是一块边长为1，周长记为P1的正三角形纸板，沿图①的底边剪去一块边长为的正三角形纸板后得到图②，然后沿同一底边依次剪去一块更小的正三角形纸板（即其边长为前一块被剪如图掉正三角形纸板边长的）后，得图③，④，…，记第n（n≥3）块纸板的周长为Pn，则P2018﹣P2017的值为（　　）

    A. B. C. D.

    【答案】C

    【解析】

    根据等边三角形的性质（三边相等）求出等边三角形的周长P1，P2，P3，P4，根据周长相减的结果能找到规律即可求出答案．

    P1=1+1+1=3，

    P2=1+1+=，

    P3=1+1+×3=，

    P4=1+1+×2+×3=，

    …

    ∴p3-p2=-==；

    P4-P3=-==，

    则Pn-Pn-1=，

    故P2018﹣P2017=

    故答案为：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：3+2=（1+）2，善于思考的小明进行了以下探索：
    设a+b=（m+n）2（其中a、b、m、n均为整数），则有a+b=m2+2n2+2mn，∴a=m2+2n2，b=2mn，这样小明就找到了一种把部分a+b的式子化为平方式的方法。
    请我仿照小明的方法探索并解决下列问题：
    （1）当a、b、m、n均为正整数时，若a+b=（m+n）2，用含m、n的式子分别表示a、b，得a=________, b=___________.

    （2）若a+4=（m+n）2，且a、m、n均为正整数，求a的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，有一座拱桥圆弧形，它的跨度AB为60米，拱高PM为18米，当洪水泛滥到跨度只有30米时，就要采取紧急措施，若拱顶离水面只有4米，即PN=4米时，是否采取紧急措施？（ =1.414）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，BC=AC，∠C=90°，直角顶点C在x轴上，一锐角顶点B在y轴上．

    （1）如图①若AD于垂直x轴，垂足为点D．点C坐标是（﹣1，0），点A的坐标是（﹣3，1），求点B的坐标．

    （2）如图②，直角边BC在两坐标轴上滑动，若y轴恰好平分∠ABC，AC与y轴交于点D，过点A作AE⊥y轴于E，请猜想BD与AE有怎样的数量关系，并证明你的猜想．

    （3）如图③，直角边BC在两坐标轴上滑动，使点A在第四象限内，过A点作AF⊥y轴于F，在滑动的过程中，请猜想OC，AF，OB之间有怎样的关系（直接写出结论，不需要证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】未成年人思想道德建设越来越受到社会的关注，辽阳青少年研究所随机调查了本市一中学100名学生寒假中花零花钱的数量(钱数取整数元)，以便引导学生树立正确的消费观．根据调查数据制成了频

    分组

    频数

    频率

    0.5～50.5

    　 　

    0.1

    50.5～　 　

    20

    0.2

    100.5～150.5

    　 　

    　 　

    　 　200.5

    30

    0.3

    200.5～250.5

    10

    0.1

    率分布表和频率分布直方图(如图)．

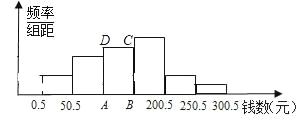
    (1)补全频率分布表；

    (2)在频率分布直方图中，长方形ABCD的面积是　 　；这次调查的样本容量是　 　；

    (3)研究所认为，应对消费150元以上的学生提出勤俭节约的建议．试估计应对该校1000名学生中约多少名学生提出这项建议．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O的直径AB=4，∠ABC=30°，BC交⊙O于D，D是BC的中点．

    （1）求BC的长；
    （2）过点D作DE⊥AC，垂足为E，求证：直线DE是⊙O的切线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读资料：
    如图1，在平面直角坐标系xOy中，A，B两点的坐标分别为A（x1 ， y1），B（x2 ， y2），由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 ， 所以A，B两点间的距离为AB= ．
    我们知道，圆可以看成到圆心的距离等于半径的点的集合，如图2，在平面直角坐标系xOy中，A （x，y）为圆上任意一点，则点A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2 ， 当⊙O的半径OA为r时，⊙O的方程可写为：x2+y2=r2 ．
    问题拓展：
    如果圆心坐标为P （a，b），半径为r，那么⊙P的方程可以写为　（x﹣a）2+（y﹣b）2=r2　 ．
    综合应用：
    如图3，⊙P与x轴相切于原点O，P点坐标为（0，6），A是⊙P上一点，连接OA，使∠POA=30°，作PD⊥OA，垂足为D，延长PD交x轴于点B，连接AB．
    ①证明AB是⊙P的切线；
    ②是否存在到四点O，P，A，B距离都相等的点Q？若存在，求Q点坐标，并写出以点Q为圆心，OQ长为半径的⊙Q的方程；若不存在，说明理由．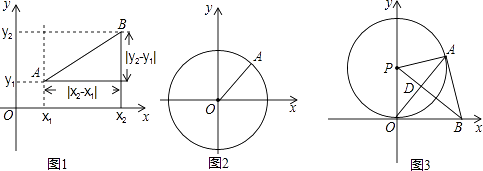

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，抛物线y=﹣2x2+（m+9）x﹣6的对称轴是x=2．
    （1）求抛物线表达式和顶点坐标；
    （2）将该抛物线向右平移1个单位，平移后的抛物线与原抛物线相交于点A，求点A的坐标；
    （3）抛物线y=﹣2x2+（m+9）x﹣6与y轴交于点C，点A关于平移后抛物线的对称轴的对称点为点B，两条抛物线在点A、C和点A、B之间的部分（包含点A、B、C） 记为图象M．将直线y=2x﹣2向下平移b（b＞0）个单位，在平移过程中直线与图象M始终有两个公共点，请你写出b的取值范围 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为应对越来越严重的雾霾天气，孔明同学所在班级的家长委员会，准备为该班集资捐赠一台大型的空气净化机，现知道某商场将该型号的空气净化机按标价的八折出售，每台空气净化机仍可获利，已知该型号客气净化机的进价为元．

    求该空气净化机的标价．

    若该班有名学生，则该班每位学生家长应平均捐助多少元．

    查看答案和解析>>

    同步练习册答案