
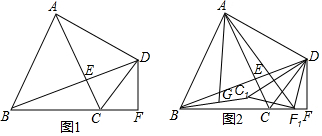
分析 (1)如图1中,作AM⊥BC于M,AN⊥DF于N,EH⊥AB于H,在BF上取一点K,使得BK=DK.由△AMB≌△AND,推出AM=AN,四边形AMFN是正方形,推出FM=FN,由Rt△ACM≌Rt△ADN,推出CM=DN,推出CF=DF=1,由∠KBD=∠KDB=15°,推出∠DKF=∠KBD+∠KDB=30°推出KD=KB=2,KF=$\sqrt{3}$,推出BF=2+$\sqrt{3}$,BC=AB=$\sqrt{3}$+1,设AE=x,则AH=$\frac{1}{2}$x,BH=HE=$\frac{\sqrt{3}}{2}$x,可得$\frac{1}{2}$x+$\frac{\sqrt{3}}{2}$x=1+$\sqrt{3}$,解方程即可解决问题.
(2)如图2中,延长FG到M,延长BA交F1C1的延长线于N,使得GM=F1G,则△GMB≌△GF1C1,只要证明△ABM≌△ADF1,即可推出△AMF1是等腰直角三角形,延长即可解决问题.
解答 (1)解:如图1中,作AM⊥BC于M,AN⊥DF于N,EH⊥AB于H,在BF上取一点K,使得BK=DK.
∵∠BAD=∠BFD=90°,
∴∠BAD+∠BFD=180°,
∴∠ABF+∠ADF=180°,∵∠ABC=60°,
∴∠ADF=120°,
∴∠ADN=60°,
在△AMB和△AND中,
$\left\{\begin{array}{l}{∠ABM=∠ADN}\\{∠AMB=∠N}\\{AB=AD}\end{array}\right.$,
∴△AMB≌△AND,
∴AM=AN,
∵四边形AMFN是矩形,
∴四边形AMFN是正方形,
∴FM=FN,
在Rt△ACM和Rt△ADN中,
$\left\{\begin{array}{l}{AC=AD}\\{AM=AN}\end{array}\right.$,
∴Rt△ACM≌Rt△ADN,
∴CM=DN,
∴CF=DF=1,
∵∠ABC=60°,∠ABD=45°,
∴∠KBD=∠KDB=15°,
∴∠DKF=∠KBD+∠KDB=30°
∴KD=KB=2,KF=$\sqrt{3}$,
∴BF=2+$\sqrt{3}$,BC=AB=$\sqrt{3}$+1,设AE=x,则AH=$\frac{1}{2}$x,BH=HE=$\frac{\sqrt{3}}{2}$x,
∴$\frac{1}{2}$x+$\frac{\sqrt{3}}{2}$x=1+$\sqrt{3}$,
∴x=2,
∴AE=2.
(2)证明:如图2中,延长F1G到M,延长BA交F1C1的延长线于N,使得GM=F1G,则△GMB≌△GF1C1,
∴BM=F1C1=DF1,∠BMG=∠GF1N,
∴BM∥F1N,
∴∠MBA=∠N,
∵∠NAO=∠OF1D=90°,∠AON=∠DOF1,
∴∠N=∠ADF1,
∴∠ABM=∠ADF1,∵AB=AD,
∴△ABM≌△ADF1,
∴AM=AF1,∠MAB=∠DAF1,
∴∠MAF1=∠BAD=90°,
∴△AMF1是等腰直角三角形,
∴AG⊥MF1,AG=GF1,
∴AF1=$\sqrt{2}$AG.
点评 本题考查旋转变换、等边三角形的性质、等腰直角三角形的性质、全等三角形的判定和性质、正方形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
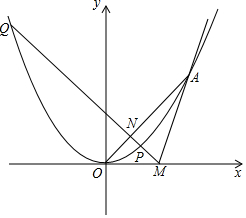 已知抛物线y=ax2(a>0),直线l:y=kx-2k,直线l与x轴交于点M,与抛物线交于唯一的公共点A(异于点O),且满足:MA=2$\sqrt{5}$,直线MQ与抛物线交于P、Q两点,与直线OA交于点N
已知抛物线y=ax2(a>0),直线l:y=kx-2k,直线l与x轴交于点M,与抛物线交于唯一的公共点A(异于点O),且满足:MA=2$\sqrt{5}$,直线MQ与抛物线交于P、Q两点,与直线OA交于点N查看答案和解析>>
科目:初中数学 来源: 题型:解答题
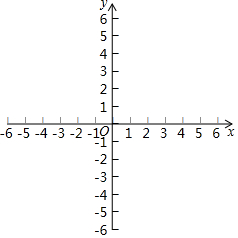 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(-2,0),B(0,-2$\sqrt{3}$),C(4,0),其中对称轴与x轴交于点D.
如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(-2,0),B(0,-2$\sqrt{3}$),C(4,0),其中对称轴与x轴交于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com