
【题目】如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC. 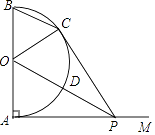
(1)求证:△OAP≌△OCP;
(2)若半圆O的半径等于2,填空: ①当AP=时,四边形OAPC是正方形;
②当AP=时,四边形BODC是菱形.
【答案】
(1)证明:∵PC切半圆O于点C,
∴OC⊥PC,
∵AM⊥AB,
∴∠OAP=90°,
在Rt△OAP和Rt△OCP中
![]() ,
,
∴Rt△OAP≌Rt△OCP
(2)2;2 ![]()
【解析】(2)解:①∵Rt△OAP≌Rt△OCP,
∴PA=PC,
而OA=OC,
∴当AO=AP时,四边形OAPC为菱形,
而∠OAP=90°,
∴四边形OAPC是正方形,
此时AP=OA=2;
②∵四边形BODC是菱形,
∴OB=OD=CD=BC,BC∥OD,
∴△OBC为等边三角形,
∴∠B=60°,
∴∠AOP=60°,
在Rt△OAP中,∵tan∠AOP= ![]() ,
,
∴AP=2tan60°=2 ![]() ,
,
即AP=2 ![]() 时,四边形BODC是菱形.
时,四边形BODC是菱形.
所以答案是2,2 ![]() .
.



科目:初中数学 来源: 题型:
【题目】2017年3月27日是全国中小学安全教育日,为了让学生了解安全知识,增强安全意识,某校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩为样本,绘制了下列两幅统计图(说明:A级:90~100分;B级:75~89分;C级:60~74分;D级:60分以下).请结合图中提供的信息,解答下列问题:
(1)本次调查共抽取了多少名学生?
(2)扇形统计图中C级所在的扇形的圆心角度数是______;
(3)请把条形统计图补充完整;
(4)若该校共有2000名学生,请你估计安全知识竞赛中A级和B级的学生一共有多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处.再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处.如图2.

(1)求证:EG=CH;
(2)已知AF=![]() ,求AD和AB的长.
,求AD和AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
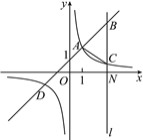
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象有公共点A(1,2),D(-2,-1).直线l⊥x轴,与x轴交于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2),D(-2,-1).直线l⊥x轴,与x轴交于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(1)求一次函数与反比例函数的表达式;
(2)求△ABC的面积;
(3)根据图象回答:当x在什么范围时,一次函数的值大于反比例函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
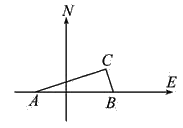
【题目】如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13nmile的A,B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120nmile,乙巡逻艇每小时航行50nmile,航向为北偏西40°,求甲巡逻艇的航向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠ACB=90°,点F是AB上一点,作等腰Rt△FCP,且∠PCF=90°,连结AP.
(1)求证:△CFB≌△CPA;
(2)求证:AP2+AF2=PF2;
(3)如图2,在AF上取点E,使∠ECF=45°,求证:AE2+BF2=EF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一个游戏的中奖概率是 ![]() ,则做100次这样的游戏一定会中奖
,则做100次这样的游戏一定会中奖
B.为了解全国中学生的心理健康情况,应该采用普查的方式
C.一组数据 8,8,7,10,6,8,9 的众数和中位数都是8
D.若甲组数据的方差s2=0.01,乙组数据的方差s2=0.1,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图: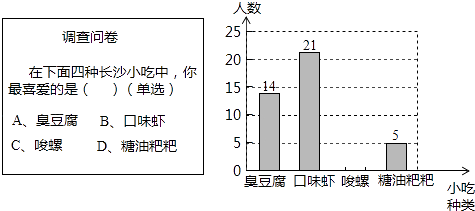
请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?
(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com