
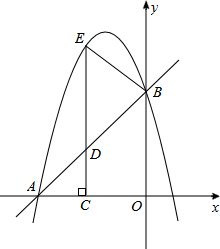
 如图,在平面直角坐标系xOy中,直线y=x+4与x轴、y轴分别交于点A,B,抛物线y=-x2+bx+c经过A、B两点,D(m,m+4)为直线AB上一动点,过点D作x轴的垂线,垂足为点C,CD的延长线交抛物线于点E,连接BE.
如图,在平面直角坐标系xOy中,直线y=x+4与x轴、y轴分别交于点A,B,抛物线y=-x2+bx+c经过A、B两点,D(m,m+4)为直线AB上一动点,过点D作x轴的垂线,垂足为点C,CD的延长线交抛物线于点E,连接BE.分析 (1)首先求出点A、B的坐标,然后利用待定系数法求出抛物线的解析式;
(2)由于△ACD为等腰直角三角形,而△DBE和△DAC相似,则△DBE必为等腰直角三角形.分两种情况讨论,要点是求出点E的坐标,由于点E在抛物线上,则可以由此列出方程求出未知数;
(3)设点C坐标为(m,0)(m<0),根据已知条件求出点E坐标为(m,8+m);由于点E在抛物线上,则可以列出方程求出m的值,进而得出点D的坐标.
解答 解:(1)在直线解析式y=x+4中,令x=0,得y=4;令y=0,得x=-4,
∴A(-4,0),B(0,4).
∵点A(-4,0),B(0,4)在抛物线y=-x2+bx+c上,
∴$\left\{\begin{array}{l}{-16-4b+c=0}\\{c=4}\end{array}\right.$,
解得:b=-3,c=4,
∴抛物线的解析式为:y=-x2-3x+4,
故答案为:-4;0;0;4;-x2-3x+4;
(2)设点C坐标为(m,0)(m<0),则OC=-m,CD=AC=4+m,BD=$\sqrt{2}$OC=-$\sqrt{2}$m,则D(m,4+m),
∵△ACD为等腰直角三角形,△DBE和△DAC相似,
∴△DBE必为等腰直角三角形,
(i)若∠BED=90°,则BE=DE,
∵BE=OC=-m,
∴DE=BE=-m,
∴CE=4+m-m=4,
∴E(m,4),
∵点E在抛物线y=-x2-3x+4上,
∴4=-m2-3m+4,解得m=0(不合题意,舍去)或m=-3,
(ii)若∠EBD=90°,则BE=BD=-$\sqrt{2}$m,
在等腰直角三角形EBD中,DE=$\sqrt{2}$BD=-2m,
∴CE=4+m-2m=4-m,
∴E(m,4-m).
∵点E在抛物线y=-x2-3x+4上,
∴4-m=-m2-3m+4,解得m=0(不合题意,舍去)或m=-2,
综上所述,存在点D,使得△DBE和△DAC相似,m的值为-2或-3;
(3)设点C坐标为(m,0)(m<0),则OC=-m,AC=4+m.
∵OA=OB=4,∴∠BAC=45°,
∴△ACD为等腰直角三角形,
∴CD=AC=4+m,
∴CE=CD+DE=4+m+4=8+m,
∴点E坐标为(m,8+m),
∵点E在抛物线y=-x2-3x+4上,
∴8+m=-m2-3m+4,解得m1=m2=-2.
∴D(-2,2).
点评 本题考查了二次函数与一次函数的图象与性质、函数图象上点的坐标特征、待定系数法、相似三角形、等腰直角三角形等重要知识点.第(2)问需要分类讨论,这是本题的难点.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
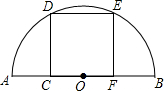 如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF.
如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com