
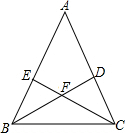
 如图,△ABC中,AB=AC,∠A=36°,∠ABC和∠ACB的平分线交于点F,则图中共有等腰三角形( )
如图,△ABC中,AB=AC,∠A=36°,∠ABC和∠ACB的平分线交于点F,则图中共有等腰三角形( )| A. | 7个 | B. | 8个 | C. | 9个 | D. | 10个 |
分析 由在△ABC中,AB=AC,∠A=36°,根据等边对等角,即可求得∠ABC与∠ACB的度数,又由BD、CE分别为∠ABC与∠ACB的角平分线,即可求得∠ABD=∠CBD=∠ACE=∠BCE=∠A=36°,然后利用三角形内角和定理与三角形外角的性质,即可求得∠BEF=∠BFE=∠ABC=∠ACB=∠CDF=∠CFD=72°,由等角对等边,即可求得答案.
解答 解:∵在△ABC中,AB=AC,∠A=36°,
∴∠ABC=∠ACB=$\frac{180°-36°}{2}$=72°,
∵BD、CE分别为∠ABC与∠ACB的角平分线,
∴∠ABD=∠CBD=∠ACE=∠BCE=∠A=36°,
∴AE=CE,AD=BD,BF=CF,
∴△ABC,△ABD,△ACE,△BFC是等腰三角形,
∵∠BEC=180°-∠ABC-∠BCE=72°,∠CDB=180°-∠BCD-∠CBD=72°,∠EFB=∠DFC=∠CBD+∠BCE=72°,
∴∠BEF=∠BFE=∠ABC=∠ACB=∠CDF=∠CFD=72°,
∴BE=BO,CF=CD,BC=BD=CF,
∴△BEF,△CDF,△BCD,△CBE是等腰三角形.
∴图中的等腰三角形有8个.
故选B.
点评 本题考查了等腰三角新的判定与性质、三角形内角和定理以及三角外角的性质.此题难度不大,解题的关键是求得各角的度数,掌握等角对等边与等边对等角定理的应用.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
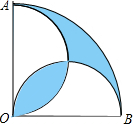 如图,在圆心角为直角的扇形OAB中,分别以OA、OB为直径作两个半圆,向直角扇形OAB内随机取一点,则该点刚好来自阴影部分的概率是1-$\frac{2}{π}$.
如图,在圆心角为直角的扇形OAB中,分别以OA、OB为直径作两个半圆,向直角扇形OAB内随机取一点,则该点刚好来自阴影部分的概率是1-$\frac{2}{π}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com