
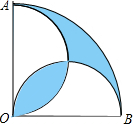
 如图,在圆心角为直角的扇形OAB中,分别以OA、OB为直径作两个半圆,向直角扇形OAB内随机取一点,则该点刚好来自阴影部分的概率是1-$\frac{2}{π}$.
如图,在圆心角为直角的扇形OAB中,分别以OA、OB为直径作两个半圆,向直角扇形OAB内随机取一点,则该点刚好来自阴影部分的概率是1-$\frac{2}{π}$. 分析 设OA的中点是D,则∠CDO=90°,这样就可以求出弧OC与弦OC围成的弓形的面积,从而可求出两个圆的弧OC围成的阴影部分的面积,用扇形OAB的面积减去两个半圆的面积,加上两个弧OC围成的面积的2倍就是阴影部分的面积,最后根据几何概型的概率公式解之即可.
解答 解:设OA的中点是D,则∠CDO=90°,半径为r
S扇形OAB=$\frac{1}{4}$πr2
S半圆OAC=$\frac{1}{2}$π($\frac{r}{2}$)2=$\frac{1}{8}$πr2
S△ODC=$\frac{1}{2}$×$\frac{r}{2}$×$\frac{r}{2}$=$\frac{1}{8}$r2
S弧OC=$\frac{1}{2}$S半圆OAC-S△ODC=$\frac{1}{16}$πr2-$\frac{1}{8}$r2
两个圆的弧OC围成的阴影部分的面积为$\frac{1}{8}$πr2-$\frac{1}{4}$r2
图中阴影部分的面积为$\frac{1}{4}$πr2-2×$\frac{1}{8}$πr2+2($\frac{1}{8}$πr2-$\frac{1}{4}$r2)=$\frac{1}{4}$πr2-$\frac{1}{2}$r2
∴该点刚好来自阴影部分的概率是:1-$\frac{2}{π}$.
故答案为:1-$\frac{2}{π}$
点评 本题主要考查了几何概型,解题的关键是求阴影部分的面积,不规则图形的面积可以转化为几个不规则的图形的面积的和或差的计算,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
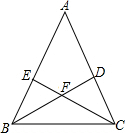 如图,△ABC中,AB=AC,∠A=36°,∠ABC和∠ACB的平分线交于点F,则图中共有等腰三角形( )
如图,△ABC中,AB=AC,∠A=36°,∠ABC和∠ACB的平分线交于点F,则图中共有等腰三角形( )| A. | 7个 | B. | 8个 | C. | 9个 | D. | 10个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com