
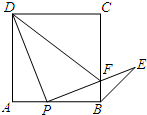
 如图,正方形ABCD的边AB上有一点P(不与A、B重合),连接PD并将线段PD绕着点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE、DF.则∠CBE的度数是
如图,正方形ABCD的边AB上有一点P(不与A、B重合),连接PD并将线段PD绕着点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE、DF.则∠CBE的度数是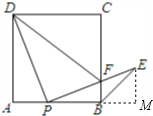 解:如图,过点E作EM⊥AB交AB的延长线于点M;
解:如图,过点E作EM⊥AB交AB的延长线于点M;
|


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:
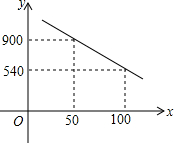 某宾馆经市场调研发现,每周该宾馆入住的房间数y与房间单价x之间存在如图所示的函数关系式.
某宾馆经市场调研发现,每周该宾馆入住的房间数y与房间单价x之间存在如图所示的函数关系式.查看答案和解析>>
科目:初中数学 来源: 题型:
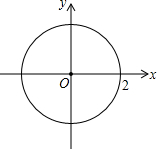 如图,⊙O的圆心是坐标原点,半径为2个单位,在坐标轴上找一点P,以P为圆心,1个单位长为半径作⊙P与⊙O相切,画出图形,并写出满足条件的所有点P的坐标.
如图,⊙O的圆心是坐标原点,半径为2个单位,在坐标轴上找一点P,以P为圆心,1个单位长为半径作⊙P与⊙O相切,画出图形,并写出满足条件的所有点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:
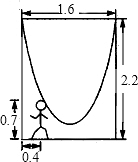 如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一根绳子的两端拴于立柱与铁结合处,绳子自然下垂呈抛物线状态,一身高0.7米的小女孩站在离立柱0.4米处,其头刚好触上绳子,则绳子最低点到地面的距离为( )米.
如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一根绳子的两端拴于立柱与铁结合处,绳子自然下垂呈抛物线状态,一身高0.7米的小女孩站在离立柱0.4米处,其头刚好触上绳子,则绳子最低点到地面的距离为( )米.| A、0.16 | B、0.2 |
| C、0.4 | D、0.64 |
查看答案和解析>>
科目:初中数学 来源: 题型:
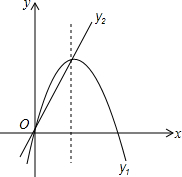 如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较大值记为M;若y1=y2,记M=y1=y2.
如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较大值记为M;若y1=y2,记M=y1=y2.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,∠EOD=70°,射线OC,OB是∠EOA、∠DOA的角平分线.
如图,∠EOD=70°,射线OC,OB是∠EOA、∠DOA的角平分线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com