【题目】已知：
分别是
的高，角平分线，
，则
的度数为________________度.
【答案】20或50
【解析】
分钝角三角形或锐角三角形两种情形分别求解即可．
解：如图，当△ABC是钝角三角形时，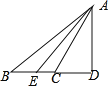
∵AD⊥BD，
∴∠ADC=90°，
∵∠ACD=60°，∠ACD=∠B+∠BAC，∠B=20°，
∴∠BAC=∠ACD -∠B =40°，∠CAD=90°-∠ACD=90°- 60°=30°
∵AE平分∠BAC，
∴∠BAE=∠CAE=
∠BAC=20°，
∴∠EAD=∠CAD+∠CAE=30°+20°=50°．
如图，当△ABC是锐角三角形时，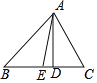
∵∠C=60°，∠B=20°，
∴∠BAC=100°，∠BAD= =90°-20°=70°，
∵AE平分∠BAC，
∴∠BAE=∠BAC=50°，
∴∠EAD=∠DAB-∠BAE=70°-50°=20°.，
综上所述：∠EAD=50°或20°．
故答案为：50或20．
科目：初中数学 来源： 题型：
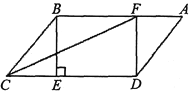
【题目】在□ABCD中，BE⊥CD于点E，点F在AB上，且AF=CE，连接DF．
(1)求证：四边形BEDF是矩形；
(2)连接CF，若CF平分∠BCD，且CE=3，BE=4，求矩形BEDF的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校开展了为期一周的“敬老爱亲”社会活动，为了解情况，学生会随机调查了部分学生在这次活动中做家务的时间，并将统计的时间（单位：小时）分成5组，A：0.5≤x＜1，B：1≤x＜1.5，C：1.5≤x＜2，D：2≤x＜2.5，E：2.5≤x＜3，制作成两幅不完整的统计图（如图）．
请根据图中提供的信息，解答下列问题：
（1）学生会随机调查了 名学生；
（2）补全频数分布直方图；
（3）若全校有900名学生，估计该校在这次活动中做家务的时间不少于2.5小时的学生有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠C＝90°，D是BC边上一点，以DB为直径的⊙O经过AB的中点E，交AD的延长线于点F，连接EF.
(1)求证：∠1＝∠F；
(2)若sinB＝
，EF＝2
，求CD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，△ABC是等边三角形，点D、E分别是边BC、CA上的点，且BD=CE，AD、BE相交于点O．
（1）求证：△BAE≌△ACD；
（2）求∠AOB的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
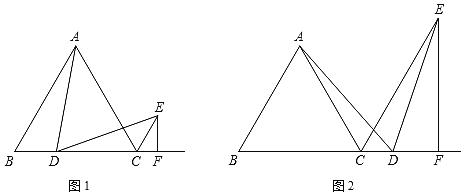
【题目】在等边△ABC中，D为射线BC上一点，CE是∠ACB外角的平分线，∠ADE=60°，EF⊥BC于F．
（1）如图1，若点D在线段BC上，证明：∠BAD=∠EDC；
（2）如图1，若点D在线段BC上，证明：①AD=DE；②BC=DC+2CF（提示：构造全等三角形）；
（3）如图2，若点D在线段BC的延长线上，直接写出BC、DC、CF三条线段之间的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在矩形ABCD中，AB＝3，BC＝2，以点A为旋转中心，逆时针旋转矩形ABCD，旋转角为α（0°＜α＜180°），得到矩形AEFG，点B、点C、点D的对应点分别为点E、点F、点G．
（1）如图①，当点E落在DC边上时，直写出线段EC的长度为 ；
（2）如图②，当点E落在线段CF上时，AE与DC相交于点H，连接AC，
①求证：△ACD≌△CAE；
②直接写出线段DH的长度为 ．
（3）如图③设点P为边FG的中点，连接PB，PE，在矩形ABCD旋转过程中，△BEP的面积是否存在最大值？若存在请直接写出这个最大值；若不存在请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
