
【题目】在矩形ABCD中,AB=3,BC=2,以点A为旋转中心,逆时针旋转矩形ABCD,旋转角为α(0°<α<180°),得到矩形AEFG,点B、点C、点D的对应点分别为点E、点F、点G.
(1)如图①,当点E落在DC边上时,直写出线段EC的长度为 ;
(2)如图②,当点E落在线段CF上时,AE与DC相交于点H,连接AC,
①求证:△ACD≌△CAE;
②直接写出线段DH的长度为 .
(3)如图③设点P为边FG的中点,连接PB,PE,在矩形ABCD旋转过程中,△BEP的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.

【答案】(1) ![]() (2) ①证明见解析,②
(2) ①证明见解析,②![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)根据勾股定理求出DE的长度,即可求解.
(2)①根据HL即可判定三角形全等.
②设![]()
![]() 在Rt△ADH中根据勾股定理即可求解.
在Rt△ADH中根据勾股定理即可求解.
(3)如图③中,连接PA,作BM⊥PE交PE的延长线于M.根据题意可得:PF=PG=![]() ,
,
则PA=PE=![]() ,S△PBE=
,S△PBE=![]() PEBM=
PEBM=![]() BM,当BM的值最大时,△PBE的面积最大,求出BM的最大值即可.
BM,当BM的值最大时,△PBE的面积最大,求出BM的最大值即可.
(1)![]()
![]()
故答案为: ![]()
(2) ①证明:如图②中,
∵当点E落在线段CF上,
∴∠AEC=∠ADC=90°,
在Rt△ADC和Rt△AEC中,
![]()
∴Rt△ACD≌Rt△CAE(HL);
②![]()
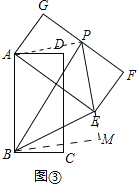
(3)存在.
理由:如图③中,连接PA,作BM⊥PE交PE的延长线于M.
由题意:PF=PG=![]() ,
,
∵AG=EF=2,∠G=∠F=90°,∴PA=PE=![]() ,
,
∴S△PBE=![]() PEBM=
PEBM=![]() BM,
BM,
∴当BM的值最大时,△PBE的面积最大,
∵BM≤PB,PB≤AB+PA,
∴PB≤3+img src="http://thumb.zyjl.cn/questionBank/Upload/2020/06/09/06/2d6c918a/SYS202006090604111882361116_DA/SYS202006090604111882361116_DA.007.png" width="9" height="33" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />=![]() ,∴BM≤
,∴BM≤![]() ,∴BM的最大值为
,∴BM的最大值为![]() ,此时点B、A、P三点共线,
,此时点B、A、P三点共线,
∴△PBE的面积的最大值为![]() .
.


科目:初中数学 来源: 题型:
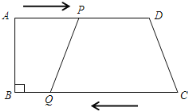
【题目】如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
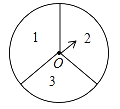
【题目】如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1,2,3三个数字.小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束后得到一组数(若指针指在分界线时重转).
(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;
(2)求每次游戏后得到的一组数恰好是方程x2﹣4x+3=0的解的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
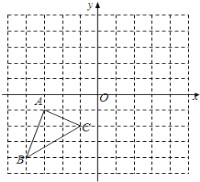
【题目】如图,正方形网格中,每个小方格都是边长为1的正方形,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)△ABC的面积为 ;
(2)将△ABC绕原点O 旋转180°,画出旋转后的△A1B1C1;
(3)将△ABC向右平移4个单位长度,画出平移后的△A2B2C2;
(4)△A1B1C1与△A2B2C2成中心对称吗?若是,请直接写出对称中心的坐标: .
查看答案和解析>>
科目:初中数学 来源: 题型:
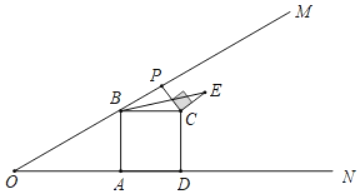
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于点A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连接BE,若AB=2,则BE的最小值为( )
A. ![]() +1B. 2
+1B. 2![]() ﹣1C. 3D. 4﹣
﹣1C. 3D. 4﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如下尚不完整的统计图.
治理杨絮一一您选哪一项?(单选)
A.减少杨树新增面积,控制杨树每年的栽种量
B.调整树种结构,逐渐更换现有杨树
C.选育无絮杨品种,并推广种植
D.对雌性杨树注射生物干扰素,避免产生飞絮
E.其他
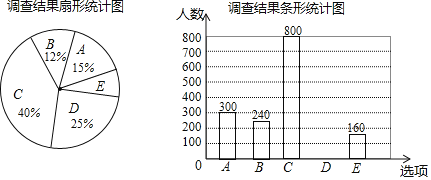
根据以上统计图,解答下列问题:
(1)本次接受调查的市民共有 人;
(2)扇形统计图中,扇形E的圆心角度数是 ;
(3)请补全条形统计图;
(4)若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)同题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC的度数.
小明想到一种方法,但是没有解答完:
如图2,过P作PE∥AB,∴∠APE+∠PAB=180°.
∴∠APE=180°-∠PAB=180°-130°=50°.
∵AB∥CD.∴PE∥CD.
…………
请你帮助小明完成剩余的解答.
(2)问题迁移:请你依据小明的思路,解答下面的问题:
如图3,AD∥BC,点P在射线OM上运动,∠MDP=∠α,∠BCP=∠β.
①当点P在A、B两点之间时,∠CPD,∠α,∠β之间有何数量关系?请说明理由.
②当点P在A、B两点外侧时(点P与点O不重合),请直接写出∠CPD,∠α,∠β之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星光厨具店购进电饭煲和电压锅两种电器进行销售其进价与售价如表
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,厨具店购进这两种电器共30台,用去了5600元,并且全部售完,问厨具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度厨具店决定采购电饭煲和电压锅共50台,且电饭煲的数量不大于电压锅的![]() ,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?
,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com