【题目】已知：如图，△ABC是等边三角形，点D、E分别是边BC、CA上的点，且BD=CE，AD、BE相交于点O．
（1）求证：△BAE≌△ACD；
（2）求∠AOB的度数．
【答案】（1）证明见解析（2）120°
【解析】
试题（1）根据等边三角形的性质求出∠BAC=∠C=60°，AC=BC，求出AE=CD，根据SAS推出全等即可；
（2）根据全等三角形的性质求出∠CAD=∠ABE，根据三角形外角性质求出∠AOE=∠BAC=60°，即可得出答案．
试题解析：（1）∵△ABC是等边三角形，
∴∠BAC=∠C=60°，BC=AC，
∵BD=CE，
∴BC-BD=AC-CE，
∴AE=CD，
在△ACD和△BAE中
∴△ACD≌△BAE（SAS）；
（2）∵△ACD≌△BAE，
∴∠CAD=∠ABE，
∴∠AOE=∠BAD+∠ABE=∠BAD+∠CAD=∠BAC=60°，
∴∠AOB=180°-60°=120°．
科目：初中数学 来源： 题型：
【题目】一个不透明的口袋里装着红、黄、绿三种只有颜色不同的球，其中红球有2个，黄球有1个，从中任意摸出1球是红球的概率为
.
（1）试求袋中绿球的个数；
（2）第1次从袋中任意摸出1球（不放回），第2次再任意摸出1球，请你用画树状图或列表格的方法，求两次都摸到红球的概率.
查看答案和解析>>
科目：初中数学 来源： 题型：
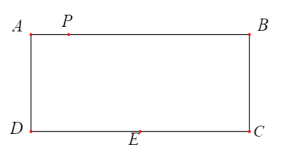
【题目】已知：如图，四边形ABCD为矩形，AB=10,BC=3,点E是CD的中点，点P在AB上以每秒2个单位的速度由A向B运动，(1)t为何值时，四边形PDEB是平行四边形？(2)点Q是直线AB上的动点，若以DEQP四点为顶点的四边形是菱形，求t值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小莹、小亮准备参加中考模拟考试,学校规定考生每人占一个桌子,按考号人座.考号按如图方式贴在桌子上,请回答下面的问题:
(1)小莹的考号是13,小亮的考号是24,在图中对应的“□”中,请用他们的名字分别标出他们在考场内座位的位置;
(2)某同学座位的位置在第a行和第b列的相交的“□”处,用数对表示是（a，b）,那么小莹的位置用数对表示是( ),小亮的位置用数对表示是( ).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，点A的坐标是（0，2），点C是x轴上的一个动点．当点C在x轴上移动时，始终保持△ACP是等边三角形（点A、C、P按逆时针方向排列）；当点C移动到点O时，得到等边三角形AOB（此时点P与点B重合）．
初步探究
(1)写出点B的坐标 ；
(2)点C在x轴上移动过程中，当等边三角形ACP的顶点P在第三象限时，连接BP，求证：△AOC≌△ABP．
深入探究
(3)当点C在x轴上移动时，点P也随之运动．探究点P在怎样的图形上运动，请直接写出结论；并求出这个图形所对应的函数表达式．
拓展应用
(4)点C在x轴上移动过程中，当△POB为等腰三角形时，直接写出此时点C的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
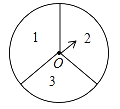
【题目】如图，有一个可以自由转动的转盘被平均分成3个扇形，分别标有1，2，3三个数字．小王和小李各转动一次转盘为一次游戏，当每次转盘停止后，指针所指扇形内的数为各自所得的数，一次游戏结束后得到一组数（若指针指在分界线时重转）．
（1）请你用树状图或列表的方法表示出每次游戏可能出现的所有结果；
（2）求每次游戏后得到的一组数恰好是方程x2﹣4x+3=0的解的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
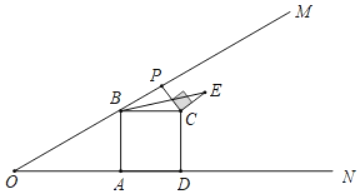
【题目】如图，已知∠MON＝30°，B为OM上一点，BA⊥ON于点A，四边形ABCD为正方形，P为射线BM上一动点，连结CP，将CP绕点C顺时针方向旋转90°得CE，连接BE，若AB＝2，则BE的最小值为（ ）
A. 
+1B. 2﹣1C. 3D. 4﹣
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义一种新运算“a*b”：当a≥b时，a*b=a+2b；当a＜b时，a*b=a-2b．
例如：3*（-4）=3+（-8）=-5，（-6）*12=-6-24=-30
（1）填空：（-4）*3= ．
（2）若（3x-4）*（x+6）=（3x-4）+2（x+6），则x的取值范围为 ；
（3）已知（3x-7）*（3-2x）＜-6，求x的取值范围；
（4）小明在计算（2x2-4x+8）*（x2+2x-2）时随意取了一个x的值进行计算，得出结果是-4，小丽告诉小明计算错了，问小丽是如何判断的．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
