
【题目】某景区游船码头派车原定于8点整准时到达景区入口接工作人员,由于汽车在路上因故障导致8:10时车还未到达景区入口,于是工作人员步行前往码头.走了一段时间后遇到了前来接他的汽车,他上车后汽车立即掉头继续前进.到达码头时已经比原计划迟到了![]() .已知汽车的速度是工作人员步行速度的6倍,则汽车在路上因故障耽误的时间为____
.已知汽车的速度是工作人员步行速度的6倍,则汽车在路上因故障耽误的时间为____![]() .
.
【答案】24.
【解析】
正常8:00到景区,出故障后,耽误t分钟,8点t分到景区,他在景区等了10分钟,车没来,就走了a分钟,在8点(10+a)分时遇到了车,他走a分钟的路程,车走![]() 分钟就走完,也就是在8点(t-
分钟就走完,也就是在8点(t-![]() )时遇到了车,得出关系式10+a=t-
)时遇到了车,得出关系式10+a=t-![]() ;
;
正常时从景区到码头用b分钟,在他遇到车的地点到景区要(b-![]() )分钟,也就是8点(t-
)分钟,也就是8点(t-![]() +b-
+b-![]() )分钟到景区,已知他是8点(b+20)分到的,得出关系式t-
)分钟到景区,已知他是8点(b+20)分到的,得出关系式t-![]() +b-
+b-![]() =b+20;联立方程组求解.
=b+20;联立方程组求解.
正常8:00准时到达景区入口,汽车在路上因故障,耽误t分钟,8点t分到达景区入口,
工作人员步行前往码头.走了10分钟,车没来,就走了a分钟,在8点(10+a)分时遇到了车;工作人员走a分钟的路程,车走![]() 分钟就走完,也就是在8点(t-
分钟就走完,也就是在8点(t-![]() )时遇到了车,有10+a=t-
)时遇到了车,有10+a=t-![]() ,
,
t=10+![]() ,-----①
,-----①
正常时从景区到码头用b分钟,
在他遇到车的地点到景区要(b-![]() )分钟,
)分钟,
也就是8点(t-![]() +b-
+b-![]() )分钟到景区,
)分钟到景区,
已知他是8点(b+20)分到的,
所以有t-![]() +b-
+b-![]() =b+20,
=b+20,
t-![]() =20,----②
=20,----②
由①②解得:a=12,t=24.
则汽车在路上因故障耽误的时间为24min.
故答案为:24.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,点D,E分别在AC,BC上,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若PF=2,则BP=( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化建设中,某学校原计划按每班5幅订购了“名人字画”共90幅.由于新学期班数增加,决定从阅览室中取若干幅“名人字画”一起分发,如果每班分4幅,则剩下17幅;如果每班分5幅,则最后一班不足3幅,但不少于1幅.
(1)该校原有的班数是多少个?
(2)新学期所增加的班数是多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两车间接到加工一批零件的任务,从开始加工到完成这项任务共用了9天,乙车间在加工2天后停止加工,引入新设备后继续加工,直到与甲车间同时完成这项任务为止,设甲、乙车间各自加工零件总数为y(件),与甲车间加工时间x(天),y与x之间的关系如图(1)所示.由工厂统计数据可知,甲车间与乙车间加工零件总数之差z(件)与甲车间加工时间x(天)的关系如图(2)所示.

(1)甲车间每天加工零件为_____件,图中d值为_____.
(2)求出乙车间在引入新设备后加工零件的数量y与x之间的函数关系式.
(3)甲车间加工多长时间时,两车间加工零件总数为1000件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】细心观察图,认真分析各式,然后解答问题:
![]() ;
;
![]() ;
;
![]() ;
;![]()

(1)请用含![]() (
(![]() 为正整数)的等式表示上述交化规律:______;
为正整数)的等式表示上述交化规律:______;
(2)观察总结得出结论:直角三角形两条直角边与斜边的关系,用一句话概括为:______;
(3)利用上面的结论及规律,请在图中作出等于![]() 的长度;
的长度;
(4)若![]() 表示三角形面积,
表示三角形面积,![]() ,
,![]() ,
,![]()
![]() ,计算出
,计算出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
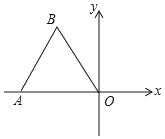
【题目】如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为2的等边三角形,以点O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,画出△OA′B′,写出点A′,B′的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com