
【题目】细心观察图,认真分析各式,然后解答问题:
![]() ;
;
![]() ;
;
![]() ;
;![]()

(1)请用含![]() (
(![]() 为正整数)的等式表示上述交化规律:______;
为正整数)的等式表示上述交化规律:______;
(2)观察总结得出结论:直角三角形两条直角边与斜边的关系,用一句话概括为:______;
(3)利用上面的结论及规律,请在图中作出等于![]() 的长度;
的长度;
(4)若![]() 表示三角形面积,
表示三角形面积,![]() ,
,![]() ,
,![]()
![]() ,计算出
,计算出![]() 的值.
的值.
【答案】(1)![]() ;(2)直角边的平方和等于斜边的平方;(3)见解析;(4)
;(2)直角边的平方和等于斜边的平方;(3)见解析;(4)![]() .
.
【解析】
(1)观察已知各式,归纳总结规律即可得;
(2)根据等式和图形即可得;
(3)先作![]() 的垂线,再在垂线上截取
的垂线,再在垂线上截取![]() ,连接
,连接![]() ,可得
,可得![]() ,同理可作出点
,同理可作出点![]() ,连接
,连接![]() 即为所求;
即为所求;
(4)先分别求出![]() 的值,再归纳总结出一般规律得出
的值,再归纳总结出一般规律得出![]() 的值,从而可得
的值,从而可得![]() 的值,然后代入求和即可.
的值,然后代入求和即可.
(1)观察已知各式可得,各式的变化规律为![]()
故答案为:![]() ;
;
(2)结合等式和图形可得,直角三角形两条直角边与斜边的关系为:直角边的平方和等于斜边的平方
故答案为:直角边的平方和等于斜边的平方;
(3)先作![]() 的垂线,再在垂线上截取
的垂线,再在垂线上截取![]() ,连接
,连接![]() ,即可得
,即可得![]() ,同理可作点
,同理可作点![]() ,连接
,连接![]() ,则
,则![]() 即为所求,如图所示:
即为所求,如图所示:

(4)![]()
![]()
![]()
归纳类推得:![]()
当![]() 时,
时,![]()
则![]()
![]()
![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】某地城管需要从甲、乙两个仓库向A、B两地分别运送10吨和5吨的防寒物资,甲、乙两仓库分别有8吨、7吨防寒物资.从甲、乙两仓库运送防寒物资到A、B两地的运费单价(元/吨)如表1,设从甲仓库运送到A地的防寒物资为x吨(如表2).
表1
甲仓库 | 乙仓库 | |
A地 | 80 | 100 |
B地 | 60 | 40 |
表2
甲仓库 | 乙仓库 | |
A地 | 10-x | |
B地 |
(1)完成表2;
(2)求运送的总运费y(元)与x(吨)之间的函数表达式,并直接写出x的取值范围;
(3)求最低总运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
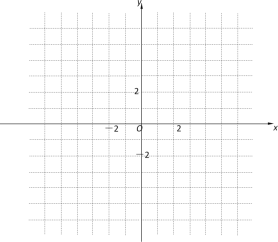
【题目】已知一次函数y1=-2x+4,完成下列问题:
(1)画出此函数的图像;
(2)将函数y1的图像向下平移2个单位,得到函数y2的图像,直接写出函数y2的表达式;
(3)当x___时,y2>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区游船码头派车原定于8点整准时到达景区入口接工作人员,由于汽车在路上因故障导致8:10时车还未到达景区入口,于是工作人员步行前往码头.走了一段时间后遇到了前来接他的汽车,他上车后汽车立即掉头继续前进.到达码头时已经比原计划迟到了![]() .已知汽车的速度是工作人员步行速度的6倍,则汽车在路上因故障耽误的时间为____
.已知汽车的速度是工作人员步行速度的6倍,则汽车在路上因故障耽误的时间为____![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某校女子田径队23人年龄的平均数和中位数都是13岁,但是后来发现其中一位同学的年龄登记错误,将14岁写成15岁,经重新计算后,正确的平均数为a岁,中位数为b岁,则下列结论中正确的是( )
A.a<13,b=13
B.a<13,b<13
C.a>13,b<13
D.a>13,b=13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若 ![]() =2,则
=2,则 ![]() 的值为( )
的值为( )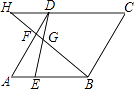
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
问题背景
在综合实践课上,老师让同学们根据如下问题情境,写出两个教学结论:
如图,点C在线段BD上,点E在线段AC上.∠ACB=∠ACD=90°,AC=BC;DC=CE,M,N分别是线段BE,AD上的点.
“兴趣小组”写出的两个教学结论是:①△BCE≌△ACD;②当CM,CN分别是△BCE和△ACD的中线时,△MCN是等腰直角三角形.
解决问题
(1)请你结合图(1).证明“兴趣小组”所写的两个结论的正确性.
类比探究
受到“兴趣小组”的启发,“实践小组”的同学们写出如下结论:如图(2),当∠BCM=∠ACN时,△MCN是等腰直角三角形.
(2)“实践小组”所写的结论是否正确?请说明理由.
感悟发现
“奋进小组”认为:当点M,N分别是BE,AD的三等分点时,△MCN仍然是等腰直角三角形请你思考:
(3)“奋进小组”所提结论是否正确?答: (填“正确”、“不正确”或“不一定正确”.)
(4)反思上面的探究过程,请你添加适当的条作,再写出使得△MCN是等腰直角三角形的数学结论.(所写结论必须正确,写出1个即可,不要求证明)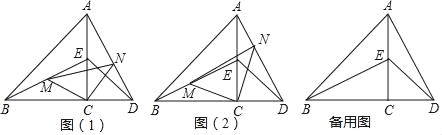
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,点0是对角线AC,BD的交点,点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足为F,连接OF,则OF的长为 . 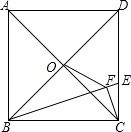
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=( )
A.4
B.5
C.4 ![]()
D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com