
【题目】如图,正方形ABCD的边长为3,点0是对角线AC,BD的交点,点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足为F,连接OF,则OF的长为 . 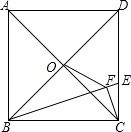
【答案】![]()
【解析】解:在BE上截取BG=CF,连接OG,如图所示:
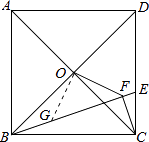
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=3,∠BCD=∠ABC=∠BAD=∠ADC=90°,OB=OC,
∵Rt△BCE中,CF⊥BE,
∴∠EBC=∠ECF,
∴∠OBG=∠OCF,
在△OBG与△OCF中, 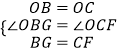 ,
,
∴△OBG≌△OCF(SAS),
∴OG=OF,∠BOG=∠COF,
∴OG⊥OF,
在Rt△BCE中,BC=DC=3,DE=2CE,
∴CE=1,
∴BE= ![]() =
= ![]() =
= ![]() ,
,
根据射影定理得:BC2=BFBE,
则32=BF ![]() ,解得:BF=
,解得:BF= ![]() ,
,
∴EF=BE﹣BF= ![]() ,
,
∵CF2=BFEF,
∴CF= ![]() ,
,
∴GF=BF﹣BG=BF﹣CF= ![]() ,
,
在等腰直角△OGF中,OF2= ![]() GF2=
GF2= ![]() ,
,
∴OF= ![]() .
.
【考点精析】本题主要考查了勾股定理的概念和正方形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】在校园文化建设中,某学校原计划按每班5幅订购了“名人字画”共90幅.由于新学期班数增加,决定从阅览室中取若干幅“名人字画”一起分发,如果每班分4幅,则剩下17幅;如果每班分5幅,则最后一班不足3幅,但不少于1幅.
(1)该校原有的班数是多少个?
(2)新学期所增加的班数是多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】细心观察图,认真分析各式,然后解答问题:
![]() ;
;
![]() ;
;
![]() ;
;![]()

(1)请用含![]() (
(![]() 为正整数)的等式表示上述交化规律:______;
为正整数)的等式表示上述交化规律:______;
(2)观察总结得出结论:直角三角形两条直角边与斜边的关系,用一句话概括为:______;
(3)利用上面的结论及规律,请在图中作出等于![]() 的长度;
的长度;
(4)若![]() 表示三角形面积,
表示三角形面积,![]() ,
,![]() ,
,![]()
![]() ,计算出
,计算出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为2的等边三角形,以点O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,画出△OA′B′,写出点A′,B′的坐标.
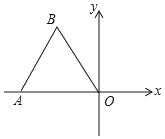
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1,
①b2>4ac;②4a﹣2b+c<0;③不等式ax2+bx+c>0的解集是x>3;④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2 .
上述判断中,正确的是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点B在原点O,直角边BC在x轴的正半轴上,∠ACB=90°,点A的坐标为(3, ![]() ),点D是BC边上一个动点(不与点B,C重合),过点D作DE⊥BC交AB边于点E,将∠ABC沿直线DE翻折,点B落在x轴上的点F处当△AEF为直角三角形时,点F的坐标是 .
),点D是BC边上一个动点(不与点B,C重合),过点D作DE⊥BC交AB边于点E,将∠ABC沿直线DE翻折,点B落在x轴上的点F处当△AEF为直角三角形时,点F的坐标是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com