
����Ŀ���ۺ���̽��
���ⱳ��
���ۺ�ʵ�����ϣ���ʦ��ͬѧ�Ǹ������������龳��д��������ѧ���ۣ�
��ͼ����C���߶�BD�ϣ���E���߶�AC�ϣ���ACB����ACD��90�㣬AC��BC��DC��CE��M��N�ֱ����߶�BE��AD�ϵĵ㣮
����ȤС�顱д����������ѧ�����ǣ��١�BCE�ա�ACD���ڵ�CM��CN�ֱ��ǡ�BCE�͡�ACD������ʱ����MCN�ǵ���ֱ�������Σ�
�������
��1��������ͼ��1����֤������ȤС�顱��д���������۵���ȷ�ԣ�
���̽��
�ܵ�����ȤС�顱����������ʵ��С�顱��ͬѧ��д�����½��ۣ���ͼ��2��������BCM����ACNʱ����MCN�ǵ���ֱ�������Σ�
��2����ʵ��С�顱��д�Ľ����Ƿ���ȷ����˵�����ɣ�
������
���ܽ�С�顱��Ϊ������M��N�ֱ���BE��AD�����ȷֵ�ʱ����MCN��Ȼ�ǵ���ֱ������������˼����
��3�����ܽ�С�顱��������Ƿ���ȷ������ �������ȷ����������ȷ����һ����ȷ������
��4����˼�����̽�����̣����������ʵ�����������д��ʹ�á�MCN�ǵ���ֱ�������ε���ѧ���ۣ�����д���۱�����ȷ��д��1�����ɣ���Ҫ��֤����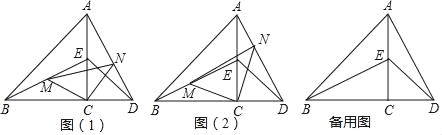
���𰸡���1������������2��ʵ��С�顱��д�Ľ�����ȷ�����ɼ���������3����һ��ȷ�����ɼ���������4���𰸲�Ψһ��������
��������
��1������BCE�ա�ACD���Ƴ�BE��AD����EBC����DAC����ΪBM��![]() BE��AN��
BE��AN��![]() AD���Ƴ�BM��AN����֤����BCM�ա�ACN�����ɽ�����⣻
AD���Ƴ�BM��AN����֤����BCM�ա�ACN�����ɽ�����⣻
��2��ʵ��С�顱��д�Ľ�����ȷ��ֻҪ֤����BCM�ա�ACN��ASA�������ɽ�����⣻
��3�����ܽ�С�顱��Ϊ������M��N�ֱ���BE��AD�����ȷֵ�ʱ����MCN��Ȼ�ǵ���ֱ�������Σ�������۲�һ��ȷ������������˵�����ɣ�
��4���𰸲�Ψһ�����磺��CM��CN�ֱ�����BCE����ACD�ĸ�ʱ����MCN�ǵ���ֱ�������Σ���CM��CN�ֱ�����BCE����ACD�Ľ�ƽ����ʱ����MCN�ǵ���ֱ��������.
��1������BCE����ACD��
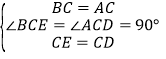 ��
��
���BCE����ACD��SAS����
��BE��AD����EBC����DAC��
��CM��CN�ֱ�����BCE����ACD�����ߣ�
��BM��![]() BE��AN��
BE��AN��![]() AD��
AD��
��BM��AN��
����BCM����ACN��
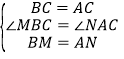 ��
��
���BCM�ա�ACN��SAS����
��CM��CN����BCM����ACN��
�ߡ�BCM+��MCE��90�㣬
���ACN+��MCE��90�㣬
��MC��CN��
���MCN�ǵ���ֱ�������Σ�
��2��ʵ��С�顱��д�Ľ�����ȷ��
���ɣ��ߡ�BCE�ա�ACD��
���EBC����DAC��
����BCM����CAN��
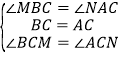 ��
��
��BCM�ա�ACN��ASA����
��CM��CN��
�ߡ�BCM+��MCE����ACB��90�㣬
���ACN+��MCE��90�㣬
��MC��CN��
���MCN�ǵ���ֱ�������Σ�
��3�����ܽ�С�顱��Ϊ������M��N�ֱ���BE��AD�����ȷֵ�ʱ����MCN��Ȼ�ǵ���ֱ�������Σ�������۲�һ��ȷ��
���ɣ���BM��![]() BE��AN��
BE��AN��![]() ADʱ����MCN��Ȼ�ǵ���ֱ�������Σ�
ADʱ����MCN��Ȼ�ǵ���ֱ�������Σ�
��BM��![]() BE��DN��
BE��DN��![]() ADʱ����MCN���ǵ���ֱ�������Σ�
ADʱ����MCN���ǵ���ֱ�������Σ�
�ʴ�Ϊ��һ��ȷ��
��4���𰸲�Ψһ�����磺��CM��CN�ֱ�����BCE����ACD�ĸ�ʱ����MCN�ǵ���ֱ�������Σ�
��CM��CN�ֱ�����BCE����ACD�Ľ�ƽ����ʱ����MCN�ǵ���ֱ�������Σ�
���ɣ�ֻҪ֤����BCM�ա�ACN��AAS���������Ƴ�����BCM����ACN���Ƴ���MCN��90�㣬
��CM��CN��
���MCN�ǵ���ֱ�������Σ�


 ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д� �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ͷ��13 800Ԫ�ʽ��ס������ֿ�Ȫˮ��500�䣬��Ȫˮ�ijɱ��ۺ����ۼ������ʾ��
���/���� | �ɱ��� | ���ۼ�(Ԫ/��) |
�� | 24 | 36 |
�� | 33 | 48 |
(1)���̳������ס������ֿ�Ȫˮ�������䣿
(2)ȫ������500���Ȫˮ�����̳�������������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABD����BDC��ƽ���߽���E��BE��CD�ڵ�F����1+��2=90������֤��

��1��AB��CD��
��2����2+��3=90����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ϸ�Ĺ۲�ͼ�����������ʽ��Ȼ�������⣺
![]() ��
��
![]() ��
��
![]() ��
��![]()

��1�����ú�![]() ��
��![]() Ϊ���������ĵ�ʽ��ʾ�����������ɣ�______��
Ϊ���������ĵ�ʽ��ʾ�����������ɣ�______��
��2���۲��ܽ�ó����ۣ�ֱ������������ֱ�DZ���б�ߵĹ�ϵ����һ�仰����Ϊ��______��
��3����������Ľ��ۼ����ɣ�����ͼ����������![]() �ij��ȣ�
�ij��ȣ�
��4����![]() ��ʾ�����������
��ʾ�����������![]() ��
��![]() ��
��![]()
![]() �������
�������![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
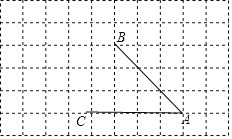
����Ŀ����ͼ������ͬ�߳���С��������ɵ�����ͼ�Σ�A��B��C���ڸ���ϣ���������ͼ����ע�����������ú�ɫǩ�ֱ���ڣ�
��1������C��AB��ƽ���ߣ�
��2������B��AC�Ĵ��ߣ�����Ϊ��G������B��AB�Ĵ��ߣ���AC���ӳ�����H��
��3����B��AC�ľ������߶� �ij��ȣ��߶�AB�ij����ǵ� ��ֱ�� �ľ��룮
��4���߶�BG��AB�Ĵ�С��ϵΪ��BG AB����������������������=������������ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
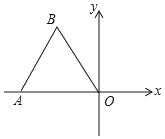
����Ŀ����ͼ����OΪƽ��ֱ������ϵ��ԭ�㣬��A��x���ϣ���OAB�DZ߳�Ϊ2�ĵȱ������Σ��Ե�OΪ��ת���ģ�����OAB��˳ʱ�뷽����ת60�㣬�õ���OA��B�䣬������OA��B�䣬д����A�䣬B������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��ͼ���һ���֣��Գ�����ֱ��x=1��
��b2��4ac����4a��2b+c��0���۲���ʽax2+bx+c��0�Ľ⼯��x��3����������2��y1������5��y2�����������ϵ����㣬��y1��y2 ��
�����ж��У���ȷ���� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У���C=90�㣬DΪAB���е㣬E��F�ֱ���AC��BC�ϣ���DE��DF.
��֤��AE2��BF2=EF2.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����һ�麬![]() �ǵ����ǰ�ABO��һ��BO����ֱ��MN�ϣ�AB����ֱ��MN���Ϸ�������
�ǵ����ǰ�ABO��һ��BO����ֱ��MN�ϣ�AB����ֱ��MN���Ϸ�������![]() ����һ�麬
����һ�麬![]() �ǵ����ǰ�POQ��һ��OQ��ֱ��MN�ϣ���һ��OP��ֱ��MN���·���
�ǵ����ǰ�POQ��һ��OQ��ֱ��MN�ϣ���һ��OP��ֱ��MN���·���

![]() �ֽ�ͼ1�е����ǰ�POQ�Ƶ�O��˳ʱ�뷽����ת����ֱ��MNǡ��Ϊ
�ֽ�ͼ1�е����ǰ�POQ�Ƶ�O��˳ʱ�뷽����ת����ֱ��MNǡ��Ϊ![]() ��ƽ����ʱ����ͼ2��ʾ����
��ƽ����ʱ����ͼ2��ʾ����![]() �Ķ���______�ȣ�
�Ķ���______�ȣ�
![]() ������ͼ2�е����ǰ��Ƶ�O��˳ʱ�뷽����ת��ͼ3��λ�ã�ʹ�ñ�OA����
������ͼ2�е����ǰ��Ƶ�O��˳ʱ�뷽����ת��ͼ3��λ�ã�ʹ�ñ�OA����![]() ���ڲ�����AOǡ��Ϊ
���ڲ�����AOǡ��Ϊ![]() ��ƽ����ʱ����
��ƽ����ʱ����![]() �Ķ�����
�Ķ�����
![]() ������ֱ�����ǰ��ͼ1��˳ʱ�뷽����ת��ͼλ��Ϊֹ����������У������ǰ�POQ�Ƶ�O��ÿ��
������ֱ�����ǰ��ͼ1��˳ʱ�뷽����ת��ͼλ��Ϊֹ����������У������ǰ�POQ�Ƶ�O��ÿ��![]() ���ٶ�������ת�������ǰ�POQ��OP��OQ������ֱ��ƽ��
���ٶ�������ת�������ǰ�POQ��OP��OQ������ֱ��ƽ��![]() �������ʱ���ǰ�POQ�Ƶ�O��ת��ʱ��t��ֵ
�������ʱ���ǰ�POQ�Ƶ�O��ת��ʱ��t��ֵ![]() ��ֱ��д����
��ֱ��д����![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com