
【题目】如图1,将一块含![]() 角的三角板ABO的一边BO放在直线MN上,AB边在直线MN的上方,其中
角的三角板ABO的一边BO放在直线MN上,AB边在直线MN的上方,其中![]() ,另一块含
,另一块含![]() 角的三角板POQ的一边OQ在直线MN上,另一边OP在直线MN的下方.
角的三角板POQ的一边OQ在直线MN上,另一边OP在直线MN的下方.

![]() 现将图1中的三角板POQ绕点O按顺时针方向旋转,当直线MN恰好为
现将图1中的三角板POQ绕点O按顺时针方向旋转,当直线MN恰好为![]() 的平分线时,如图2所示,则
的平分线时,如图2所示,则![]() 的度数______度;
的度数______度;
![]() 继续将图2中的三角板绕点O按顺时针方向旋转至图3的位置,使得边OA落在
继续将图2中的三角板绕点O按顺时针方向旋转至图3的位置,使得边OA落在![]() 的内部,且AO恰好为
的内部,且AO恰好为![]() 的平分线时,求
的平分线时,求![]() 的度数;
的度数;
![]() 在上述直角三角板从图1按顺时针方向旋转至图位置为止,这个过程中,若三角板POQ绕点O以每秒
在上述直角三角板从图1按顺时针方向旋转至图位置为止,这个过程中,若三角板POQ绕点O以每秒![]() 的速度匀速旋转,当三角板POQ的OP边或OQ边所在直线平分
的速度匀速旋转,当三角板POQ的OP边或OQ边所在直线平分![]() ,则求此时三角板POQ绕点O旋转的时间t的值
,则求此时三角板POQ绕点O旋转的时间t的值![]() 请直接写出答案
请直接写出答案![]() .
.
【答案】(1)75;(2)![]() ;(3)当OP边所在直线平分
;(3)当OP边所在直线平分![]() 时旋转时间为5秒或17秒,当OQ边所在直线平分
时旋转时间为5秒或17秒,当OQ边所在直线平分![]() 时旋转时间为11秒或23秒.
时旋转时间为11秒或23秒.
【解析】
(1)根据三角板PQO的特性结合题意可得出∠POM=45°,在平角MON中可求出∠AOP的度数;
(2)根据角平分线的定义即可得到结论;
(3)此题分两种情况,一种OP边所在直线平分∠AOB,另一种OQ边所在直线平分∠AOB,找出两种情况下三角板PQO绕点O旋转的度数,即可求出时间t.
解:![]() 直线MN平分
直线MN平分![]() ,
,![]() ,
,
![]() ,
,
又![]() 且
且![]() 为平角,
为平角,
![]() ,
,
故![]() 的度数为
的度数为![]() ;
;
故答案为:75;
![]() 恰好为
恰好为![]() 的平分线,
的平分线,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 根据题意可知,分两种情况,
根据题意可知,分两种情况,
![]() 当OP边所在直线平分
当OP边所在直线平分![]() 时,三角板PQO绕点O旋转的度数为
时,三角板PQO绕点O旋转的度数为![]() 或
或![]() ,
,
![]() ,
,
![]() 时间
时间![]() 秒
秒![]() 或
或![]() 秒
秒![]() ;
;
![]() 当OQ边所在直线平分
当OQ边所在直线平分![]() 时,三角板PQO绕点O旋转的度数为
时,三角板PQO绕点O旋转的度数为![]() 或
或![]() ,
,
![]() ,
,
![]() 时间
时间![]() 秒
秒![]() 或
或![]() 秒
秒![]() .
.
综合![]() 得当OP边所在直线平分
得当OP边所在直线平分![]() 时旋转时间为5秒或17秒,当OQ边所在直线平分
时旋转时间为5秒或17秒,当OQ边所在直线平分![]() 时旋转时间为11秒或23秒.
时旋转时间为11秒或23秒.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:初中数学 来源: 题型:
【题目】综合与探究
问题背景
在综合实践课上,老师让同学们根据如下问题情境,写出两个教学结论:
如图,点C在线段BD上,点E在线段AC上.∠ACB=∠ACD=90°,AC=BC;DC=CE,M,N分别是线段BE,AD上的点.
“兴趣小组”写出的两个教学结论是:①△BCE≌△ACD;②当CM,CN分别是△BCE和△ACD的中线时,△MCN是等腰直角三角形.
解决问题
(1)请你结合图(1).证明“兴趣小组”所写的两个结论的正确性.
类比探究
受到“兴趣小组”的启发,“实践小组”的同学们写出如下结论:如图(2),当∠BCM=∠ACN时,△MCN是等腰直角三角形.
(2)“实践小组”所写的结论是否正确?请说明理由.
感悟发现
“奋进小组”认为:当点M,N分别是BE,AD的三等分点时,△MCN仍然是等腰直角三角形请你思考:
(3)“奋进小组”所提结论是否正确?答: (填“正确”、“不正确”或“不一定正确”.)
(4)反思上面的探究过程,请你添加适当的条作,再写出使得△MCN是等腰直角三角形的数学结论.(所写结论必须正确,写出1个即可,不要求证明)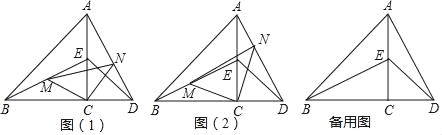
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱底面半径为![]() cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A. 12cm B. ![]() cm C. 15cm D.
cm C. 15cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=( )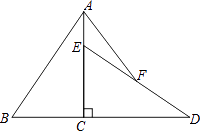
A.4
B.5
C.4 ![]()
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校园安全问题已成为社会各界关注的热点问题,区教育局要求各学校加强对学生的安全教育,教育局安全科为了调查学生对“安全知识”内容的了解程度![]() 程度分为:“A:十分熟悉”、“B:了解较多”、“C:了解较少、D:不了解”
程度分为:“A:十分熟悉”、“B:了解较多”、“C:了解较少、D:不了解”![]() ,对某所中学的学生进行了抽样调查
,对某所中学的学生进行了抽样调查![]() 我们将这次调查的结果绘制了以下两幅不完整统计图,如图1,图2,请你根据图中提供的信息解答下列问题:
我们将这次调查的结果绘制了以下两幅不完整统计图,如图1,图2,请你根据图中提供的信息解答下列问题:

根据以上信息,解答下列问题
![]() 补全条形统计图;
补全条形统计图;
![]() 本次抽样调查了______名学生;在图1中扇形统计图中,求出“D”的部分所对应的圆心角等于______度
本次抽样调查了______名学生;在图1中扇形统计图中,求出“D”的部分所对应的圆心角等于______度![]()
![]() 若该中学共有2000名学生,请你估计这所中学的所有学生中,对“安全知识”内容的了解程度为“A:十分熟悉”和“B:了解较多”的学生共有______名?
若该中学共有2000名学生,请你估计这所中学的所有学生中,对“安全知识”内容的了解程度为“A:十分熟悉”和“B:了解较多”的学生共有______名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b在数轴上的对应点如图所示,则下列式子中错误的是( )
![]()
A. a+b<0 B. a-b<0
C. -a<-b D. |a-b|=b-a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC.
理由如下:∵AD⊥BC于D,EG⊥BC于G,(_______)
∴∠ADC=∠EGC=90°,(垂直的定义),
∴AD∥EG,(_______)
∴∠1=∠2,(_______)
∠E=∠3,(_______)
又∵∠E=∠1(已知),
∴______=_______,(______)
∴AD平分∠BAC.(_______)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C,D为矩形的四个顶点,AB=16 cm,BC=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,点Q以2 cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.问几秒时点P和点Q的距离是10 cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
如图,已知∠1、∠2互为补角,且∠3=∠B,
求证:∠AED=∠ACB.
证明:∵∠1+∠2=180°,∠2+∠4=180°
∴∠1=∠4 (______)
∴AB∥EF(_______)
∴∠3=______(______)
又∠3=∠B
∴∠B=_______(_______)
∴DE∥BC (________)
∴∠AED=∠ACB (_______)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com