【题目】如图，已知Rt△ABC中，∠ACB=90°，AC=6，BC=4，将△ABC绕直角顶点C顺时针旋转90°得到△DEC．若点F是DE的中点，连接AF，则AF=（ ）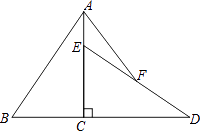
A.4
B.5
C.4 
D.6
科目：初中数学 来源： 题型：
【题目】细心观察图，认真分析各式，然后解答问题：
；
；
；
（1）请用含
（为正整数）的等式表示上述交化规律：______；
（2）观察总结得出结论：直角三角形两条直角边与斜边的关系，用一句话概括为：______；
（3）利用上面的结论及规律，请在图中作出等于
的长度；
（4）若
表示三角形面积，
，
，
，计算出
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE相交于F．
求证：AF平分∠BAC．
【答案】证明见解析.
【解析】试题分析：先根据AB=AC，可得∠ABC=∠ACB，再由垂直，可得90°的角，在△BCE和△BCD中，利用内角和为180°，可分别求∠BCE和∠DBC，利用等量减等量差相等，可得FB=FC，再易证△ABF≌△ACF，从而证出AF平分∠BAC．
试题解析：证明：∵AB=AC(已知)，
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高，
∴BD⊥AC,CE⊥AB(高的定义).
∴∠CEB=∠BDC=90°.
∴∠ECB=90°∠ABC,∠DBC=90°∠ACB.
∴∠ECB=∠DBC(等量代换).
∴FB=FC(等角对等边)，
在△ABF和△ACF中，
，
∴△ABF≌△ACF(SSS)，
∴∠BAF=∠CAF(全等三角形对应角相等)，
∴AF平分∠BAC.
【题型】解答题
【结束】
23
【题目】如图，在△ABC中，AC=BC，∠C=90°，AD是△ABC的角平分线，DE⊥AB，垂足为E．
（1）求证：CD=BE；
（2）已知CD=2，求AC的长；
（3）求证：AB=AC+CD．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下面一列有序数对：(1,1)，(1,2)，(2,1)，(1,3)，(2,2)，(3,1)，(1,4)，(2,3)，(3,2)，(4,1)，(1,5)，(2,4)，…，按这些规律，第50个有序数对是( )
A. (3,8)B. (4,7)C. (5,6)D. (6,5)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，将一块含
角的三角板ABO的一边BO放在直线MN上，AB边在直线MN的上方，其中
，另一块含
角的三角板POQ的一边OQ在直线MN上，另一边OP在直线MN的下方．
现将图1中的三角板POQ绕点O按顺时针方向旋转，当直线MN恰好为
的平分线时，如图2所示，则
的度数______度；
继续将图2中的三角板绕点O按顺时针方向旋转至图3的位置，使得边OA落在
的内部，且AO恰好为的平分线时，求
的度数；
在上述直角三角板从图1按顺时针方向旋转至图位置为止，这个过程中，若三角板POQ绕点O以每秒
的速度匀速旋转，当三角板POQ的OP边或OQ边所在直线平分
，则求此时三角板POQ绕点O旋转的时间t的值
请直接写出答案
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，Rt△ABC的顶点B在原点O，直角边BC在x轴的正半轴上，∠ACB=90°，点A的坐标为（3， 
），点D是BC边上一个动点（不与点B，C重合），过点D作DE⊥BC交AB边于点E，将∠ABC沿直线DE翻折，点B落在x轴上的点F处当△AEF为直角三角形时，点F的坐标是 ． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一块直角三角板
放置在锐角
上，使得该三角板的两条直角边
恰好分别经过点
（1）如图①，若
时，点
在内，则
度，
____度，
度；
（2）如图②，改变直角三角板的位置，使点在内，请探究
与
之间存在怎样的数量关系，并验证你的结论；
（3）如图③，改变直角三角板的位置，使点在外，且在
边的左侧，直接写出
三者之间存在的数量关系．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
