练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．若a是有理数，则下列判断正确的是（　　）
    A．|a|是正数B．-a是负数C．|a|是正数或0D．|-a|是负数或0

    分析 根据绝对值非负数的性质对各选项分析判断后利用排除法．

    解答 解：A、a=0时，|a|=0，不是正数，故本选项错误；
    B、a＜0时，-a是正数，故本选项错误；
    C、|-a|是非负数，正确；
    D、a=0时，a=-a，a＜0时，a＜-a，故本选项错误．
    故选C．

    点评 本题主要考查了绝对值非负数的性质以及数字表示数的意义，是基础题，比较简．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    3．（2×102）2=4×104；（-3×103）3=-27×109．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，△ABC是等腰直角三角形，BC=AC，直角顶点C在x轴上，以锐角顶点B在y轴上．
    （1）如图（1）若点C的坐标是（2，0），点A的坐标是（-2，-2），求B点的坐标．
    （2）如图（2），若y轴恰好平分∠ABC，AC与y轴交于点D，过点A作AE⊥y轴于E，问BD与AE之间有怎样的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，已知AB∥DE，AB⊥FC，垂足为点B，AC=DF，FE=CB．求证：∠C=∠F．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

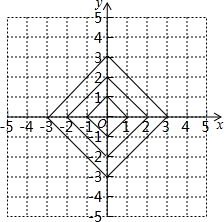    5．在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点，如图，由里向外数的第2各正方形开始，分别是由第1个正方形各顶点的横坐标和纵坐标分别乘1，2，3，…得到的，请你观察图形，猜想由里向外第12个正方形四条边上的整点个数为48．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

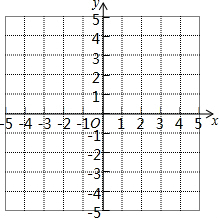    15．如图是建有平面直角坐标系的正方形网格，请按下列要求操作：
    （1）画△ABC，使A，B，C三点的坐标分别为（3，1），（4，-1），（2，-2）；
    （2）如果将△ABC向左平移4个单位长度，再向上平移3个单位长度，得到△A1B1C1．画出平移后的图形，并指出A1、B1、C1的坐标；
    （3）求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

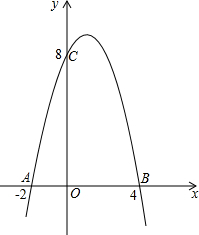    2．已知抛物线y=ax2+bx+c 与x轴交于A（-2，0），B（4，0），与y轴交于C（0，8），点M为抛物线对称轴上的点．
    （1）求抛物线解析式；
    （2）若△MAC周长最小，请求出点M的坐标；
    （3）若△MAC为直角三角形，请直接写出点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．半径为6和8的两圆相交，圆心距为10，那么公共弦的长为9.6．

    查看答案和解析>>

    科目：初中数学 来源：2017届江苏省盐都市九年级下学期第一次学情调研数学试卷（解析版） 题型：解答题

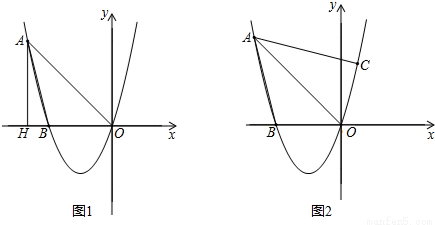
    已知，经过点A（－4，4）的抛物线y=ax2+bx+c与x轴相交于点B（－3，0）及原点O．

    （1）求抛物线的解析式；

    （2）如图1，过点A作AH⊥x轴，垂足为H，平行于y轴的直线交线段AO于点Q，交抛物线于点P，当四边形AHPQ为平行四边形时，求∠AOP的度数；

    （3）如图2，若点C在抛物线上，且∠CAO＝∠BAO，试探究：在（2）的条件下，是否存在点G，使得△GOP∽△COA？若存在，请求出所有满足条件的点G坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案