
【题目】如图1,在![]() 中,
中,![]() 于点
于点![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,
,![]() .
.
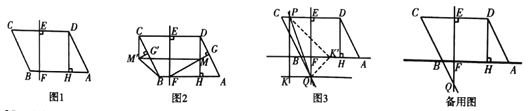
(1)如图2,作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 方向平移,得到
方向平移,得到![]() ,连接
,连接![]() .
.
①求四边形![]() 的面积;
的面积;
②直线![]() 上有一动点
上有一动点![]() ,求
,求![]() 周长的最小值.
周长的最小值.
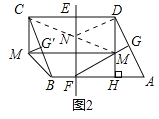
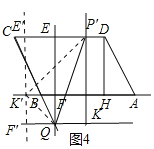
(2)如图3.延长![]() 交
交![]() 于点
于点![]() .过点
.过点![]() 作
作![]() ,过
,过![]() 边上的动点
边上的动点![]() 作
作![]() ,并与
,并与![]() 交于点
交于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,使点
翻折,使点![]() 的对应点
的对应点![]() 恰好落在直线
恰好落在直线![]() 上,求线段
上,求线段![]() 的长.
的长.
【答案】(1)①![]() ;②
;②![]() 周长的最小值为9;(2)
周长的最小值为9;(2)![]() 的长为
的长为![]() 或
或![]() .
.
【解析】(1)①根据相似三角形的判定和性质以及平移的性质进行解答即可;
②连接CM交直线EF于点N,连接DN,利用勾股定理解答即可;
(2)分点P在线段CE上和点P在线段ED上两种情况进行解答.
(1)①在ABCD中,AB=6,直线EF垂直平分CD,
∴DE=FH=3,
又BF:FA=1:5,
∴AH=2,
∵Rt△AHD∽Rt△MHF,
∴![]() ,即
,即![]() ,
,
∴HM=1.5,
根据平移的性质,MM'=CD=6,连接BM,如图1,
四边形BHMM′的面积=![]() ×6×1.5+
×6×1.5+![]() ×4×1.5=7.5;
×4×1.5=7.5;
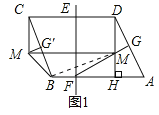
②连接CM交直线EF于点N,连接DN,如图2,
∵直线EF垂直平分CD,
∴CN=DN,
∵MH=1.5,
∴DM=2.5,
在Rt△CDM中,MC2=DC2+DM2,
∴MC2=62+(2.5)2,
即MC=6.5,
∵MN+DN=MN+CN=MC,
∴△DNM周长的最小值为9.
(2)∵BF∥CE,
∴![]() ,
,
∴QF=2,
∴PK=PK'=6,
过点K'作E'F'∥EF,分别交CD于点E',交QK于点F',如图3,
当点P在线段CE上时,
在Rt△PK'E'中,
PE'2=PK'2-E'K'2,
∴PE′=2![]() ,
,
∵Rt△PE'K'∽Rt△K'F'Q,
∴![]() ,即
,即![]() ,
,
解得:QF′=![]() ,
,
∴PE=PE'-EE'=2![]()
![]() =
=![]() ,
,
∴CP=![]() ,
,
同理可得,当点P在线段DE上时,CP′=![]() ,如图4,
,如图4,
综上所述,CP的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)已知A.B是直线上的两点,且AB=6,若P在这条直线上,且PA=5.
①画出P点在直线AB上的大致位置图;
②求PB长.
(2)尺规作图(不写作法.保留作图痕迹)
已知线段![]() ,求作:线段MN,使MN=
,求作:线段MN,使MN=![]() .
.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图①, ![]() ,试说明
,试说明![]() .下面给出了这道题的解题过程,请在下列解答中,填上适当的理由.
.下面给出了这道题的解题过程,请在下列解答中,填上适当的理由.
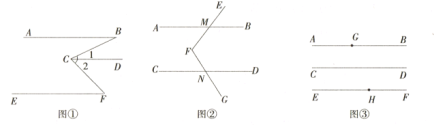
解: ∵![]() .(已知)
.(已知)
∴ ![]() .( )
.( )
同理可证, ![]() .
.
∵ ![]() ,
,
∴![]() .( )
.( )
应用:如图②, ![]() ,点
,点![]() 在
在![]() 之间,
之间,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的大小为_____________度.
的大小为_____________度.
拓展:如图③,直线![]() 在直线
在直线![]() 之间,且
之间,且![]() ,点
,点![]() 分别在直线
分别在直线![]() 上,点
上,点![]() 是直线
是直线![]() 上的一个动点,且不在直线
上的一个动点,且不在直线![]() 上,连结
上,连结![]() .若
.若![]() ,则
,则![]() =________度.
=________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2![]() ,AC=2
,AC=2![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某项工程由甲乙两队分别单独完成,则甲队用时是乙队的1.5倍:若甲乙两队合作,则需12天完成,请问:
(1)甲,乙两队单独完成各需多少天;
(2)若施工方案是甲队先单独施工![]() 天,剩下工程甲乙两队合作完成,若甲队施工费用为每天1.5万元,乙队施工费为每天3.5万元求施工总费用
天,剩下工程甲乙两队合作完成,若甲队施工费用为每天1.5万元,乙队施工费为每天3.5万元求施工总费用![]() (万元)关于施工时间
(万元)关于施工时间![]() (天)的函数关系式
(天)的函数关系式
(3)在(2)的方案下,若施工期定为15~18天内完成(含15和18天),如何安排施工方案使费用最少,最少费用为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年级学习压力大,放学后在家自学时间较初一、初二长,为了解学生学习时间,该年级随机抽取25%的学生问卷调查,制成统计表和扇形统计图,请你根据图表中提供的信息回答下列问题:
学习时间(h) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
人数 | 72 | 36 | 54 | 18 |
(1)初三年级共有学生_____人.
(2)在表格中的空格处填上相应的数字.
(3)表格中所提供的学生学习时间的中位数是_____,众数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在边BC,CD上,且BE=CF.连接AE,BF,AE与BF交于点G.下列结论错误的是( )
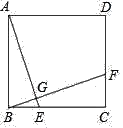
A. AE=BF B. ∠DAE=∠BFC
C. ∠AEB+∠BFC=90° D. AE⊥BF
查看答案和解析>>
科目:初中数学 来源: 题型:
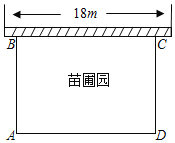
【题目】某中学课外兴趣活动小组准备围建一个矩形的苗圃圆.其中一边靠墙,另外三边用长为40m的篱笆围成.已知墙长为18m(如图所示),设这个苗圃园垂直于墙的一边AB为xm
(1)用含有x的式子表示AD,并写出x的取值范围;
(2)若苗圃园的面积为192m2平方米,求AB的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com