
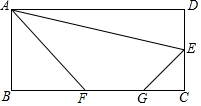
 矩形ABCD中,AB=4,BC=8,E是CD的中点,F、G是BC上的两个动点,FG=3,则四边形AFGE周长最小时,CG=$\frac{5}{3}$.
矩形ABCD中,AB=4,BC=8,E是CD的中点,F、G是BC上的两个动点,FG=3,则四边形AFGE周长最小时,CG=$\frac{5}{3}$. 分析 作E关于BC的对称点M,在AD上截取AH=3,然后连接HM交BC于G,接着在GB上截取GF=3,在矩形ABCD中,AB=4,BC=8,E为边CD的中点,得到CE=CM=2,MD=6,而AH=3,求得DH=5,然后根据相似三角形的性质即可得到结论.
解答 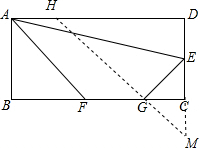 解:∵G为BC上的一个动点,
解:∵G为BC上的一个动点,
∴如图,作E关于BC的对称点M,在AD上截取AH=3,然后连接HM交BC于G,接着在GB上截取GF=3,
那么G、F两点即可满足使四边形AFGE的周长最小.
∵在矩形ABCD中,AB=4,BC=8,E为边CD的中点,
∴CE=CM=2,MD=6,而AH=3,
∴DH=5,
而BC∥AD,
∴△CGM∽△DHM,
∴CG:HD=MC:MD,
∴CG=$\frac{DH•MC}{MD}$=$\frac{5}{3}$,
故答案为:$\frac{5}{3}$.
点评 此题分别考查了轴对称-最短路程问题、勾股定理、矩形及相似三角形的性质等知识,有点难度,要求学生平时加强训练.


科目:初中数学 来源: 题型:选择题
| A. | 三个内角之比为1:2:3 | B. | 一边上的中线等于该边的一半 | ||
| C. | 三边为$\frac{1}{3}$、$\frac{1}{4}$、$\frac{1}{5}$ | D. | 三边长为m2+n2、m2-n2、2mn(m≠0,n≠0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 摸出的是3个白球 | B. | 摸出的是3个黑球 | ||
| C. | 摸出的是2个白球、1个黑球 | D. | 摸出的是2个黑球、1个白球 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{33}{100}$ | B. | $\frac{11}{100}$ | C. | $\frac{11}{99}$ | D. | $\frac{33}{101}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com