
| A. | $\frac{33}{100}$ | B. | $\frac{11}{100}$ | C. | $\frac{11}{99}$ | D. | $\frac{33}{101}$ |
分析 令n=1、2、3…,求出a1,a2,…的值,在表示出a2-1,a3-1,…从而得出规律,再提取$\frac{1}{3}$后利用拆项法解答.
解答 解:根据题意,当n=1时,a1=13=1,
当n=2时,a1+a2=23,a2=23-1=7,
所以a2-1=7-1=6=3×(1×2),
当n=3时,a1+a2+a3=33,a3=33-23=19,
所以a3-1=19-1=18=3×(2×3),
当n=4时,a1+a2+a3+a4=43,a4=43-33=37,
所以a4-1=37-1=36=3×(3×4),
…
a100=1003-993
=(100-99)×(1002+100×99+992)
=1002+100×(100-1)+(100-1)2
=1002+1002-100+1002-200+1
=3×1002-300+1,
所以a100-1=3×1002-300+1-1=100×(300-3)=100×297=3×(99×100),
$\frac{1}{{a}_{2}-1}$+$\frac{1}{{a}_{3}-1}$+…+$\frac{1}{{a}_{100}-1}$
=$\frac{1}{3×(1×2)}$+$\frac{1}{3×(2×3)}$+$\frac{1}{3×(3×4)}$+…+$\frac{1}{3×(99×100)}$
=$\frac{1}{3}$(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{99}$-$\frac{1}{100}$)
=$\frac{1}{3}$×(1-$\frac{1}{100}$)
=$\frac{1}{3}$×$\frac{99}{100}$
=$\frac{33}{100}$,
故选:A.
点评 本题考查了数字的变化规律,令n=1、2、3…,分别求出a2-1,a3-1,a4-1,…,a100-1并发现规律是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
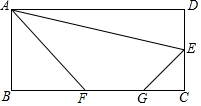 矩形ABCD中,AB=4,BC=8,E是CD的中点,F、G是BC上的两个动点,FG=3,则四边形AFGE周长最小时,CG=$\frac{5}{3}$.
矩形ABCD中,AB=4,BC=8,E是CD的中点,F、G是BC上的两个动点,FG=3,则四边形AFGE周长最小时,CG=$\frac{5}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com