
分析 先化简题目中的式子,然后将a的值代入化简后的式子即可解答本题.
解答 解:$\frac{{a}^{2}-1}{{a}^{2}-2a+1}$+$\frac{2a-{a}^{2}}{a-2}$÷a
=$\frac{(a+1)(a-1)}{(a-1)^{2}}+\frac{a(2-a)}{a-2}×\frac{1}{a}$
=$\frac{a+1}{a-1}+(-1)$
=$\frac{a+1-a+1}{a-1}$
=$\frac{2}{a-1}$,
当a=$\frac{3}{2}$时,原式=$\frac{2}{\frac{3}{2}-1}$=$\frac{2}{\frac{1}{2}}$=4.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的计算方法.


科目:初中数学 来源: 题型:解答题
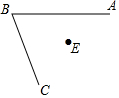 如图,∠ABC的内部有一点E
如图,∠ABC的内部有一点E查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{33}{100}$ | B. | $\frac{11}{100}$ | C. | $\frac{11}{99}$ | D. | $\frac{33}{101}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
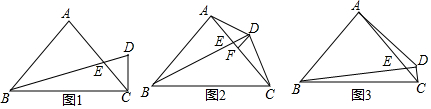
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点O是∠APB内的一点,M,N分别是点O关于PA、PB的对称点,连接MN,与PA、PB分别相交于点E、F,已知MN=6cm.
如图,已知点O是∠APB内的一点,M,N分别是点O关于PA、PB的对称点,连接MN,与PA、PB分别相交于点E、F,已知MN=6cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com