
【题目】如图1所示,四边形ABCD是正方形,点E是边BC的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,.
(1)求证:∠BAE=∠FEC
(2)取边AB的中点G,连接EG,求证:EG=CF;
(3)将△ECF绕点E逆时针旋转90° 得△EC′A, 如图2,指出AC′与EG的位置关系,并说明理由.


【答案】(1)证明见解析;(2)证明见解析;(3)AC′//EG.
【解析】试题分析:(1)由同角的余角相等,即可得到结论;
(2)用ASA证明△AGE≌△ECF即可;
(3)结论:AC′//EG.证明四边形AGEC′为平行四边形即可.
试题解析:解:(1)四边形ABCD是正方形,∴∠B =90°,∠AEB+∠BAE=90°.
∵∠AEF=90°,∴∠AEB+∠CEF=90°,∴∠BAE=∠CEF;
(2)∵四边形ABCD是正方形,∴AB=BC,∠B=∠BCD=∠DCG=90°.
∵取AB的中点G,点E是边BC的中点,∴AG=EC=BE,∴∠BGE=∠BEG=45°,∴∠AGE=135°.
∵CF平分∠DCG,∴∠DCF=∠FCG=45°,∴∠ECF=180°-∠FCG=135°,∴∠AGE=∠ECF.
因为∠GAE=∠CEF,∴△AGE≌△ECF(ASA),∴EG=CF;
(3)AC′与EG的位置关系是:AC′//EG.
∵∠C′EC=∠B=90°,∴AG//C′E.
∵AG=C′E,∴四边形AGEC′为平行四边形,∴AC′//EG.


科目:初中数学 来源: 题型:
【题目】数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是( )

A. 勾股定理 B. 直径所对的圆周角是直角
C. 勾股定理的逆定理 D. 90°的圆周角所对的弦是直径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面每组数分别是三根小木棒的长度,它们能摆成三角形的是( )
A.12cm,3cm,6cm
B.8cm,16cm,8cm
C.6cm,6cm,13cm
D.2cm,3cm,4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图11的四边形ABCD,并写出了如下不完整的已知和求证。
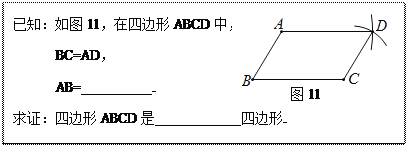

(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的想法写出证明;
证明:
(3)用文字叙述所证命题的逆命题为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究;
(![]() )如图,
)如图, ![]() 、
、![]() 为
为![]() 的边
的边![]() 、
、![]() 上的两定点,在
上的两定点,在![]() 上求作一点
上求作一点![]() ,使
,使![]() 的周长最短.(不写作法)
的周长最短.(不写作法)

(![]() )如图,矩形
)如图,矩形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,点
的中点,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的动点,求四边形
上的动点,求四边形![]() 周长的最小值.
周长的最小值.

(![]() )如图,正方形
)如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 为
为![]() 边中点,在边
边中点,在边![]() 、
、![]() 、
、![]() 上分别确定点
上分别确定点![]() 、
、![]() 、
、![]() .使得四边形
.使得四边形![]() 周长最小,并求出最小值.
周长最小,并求出最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com